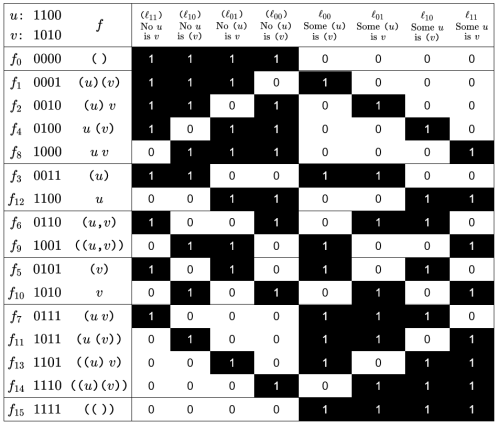
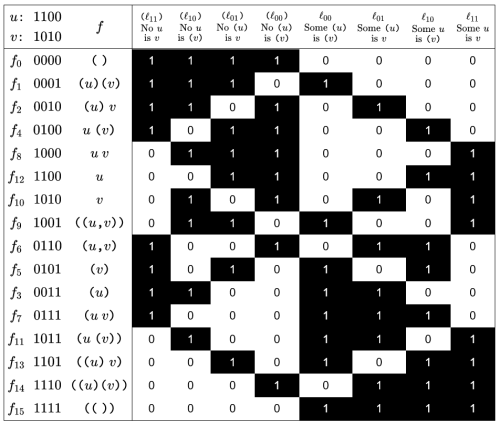
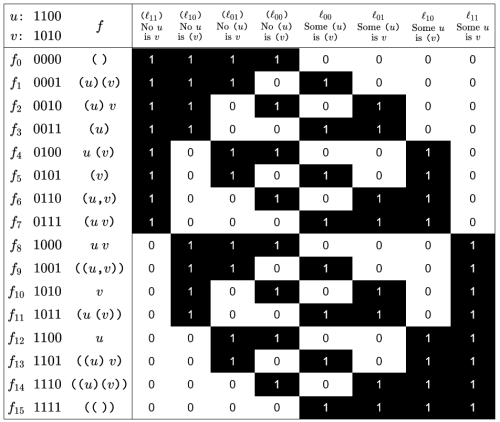
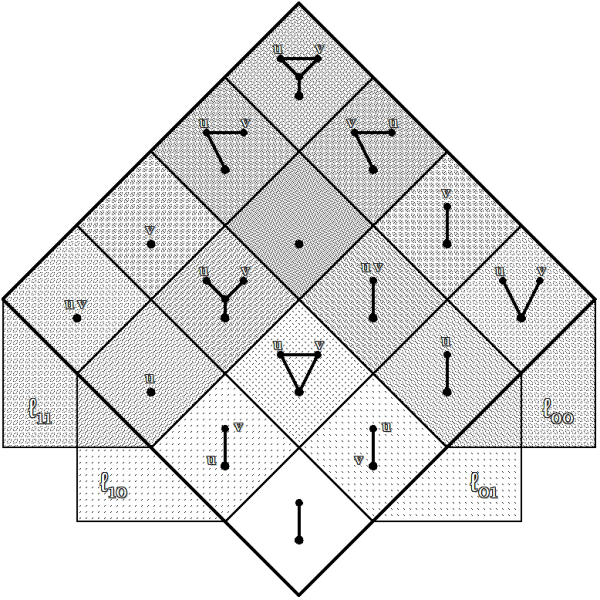
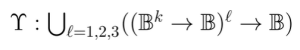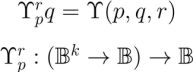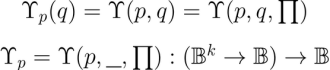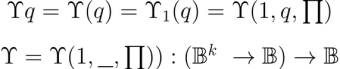The 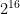 measures of type
measures of type 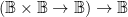 present a formidable array of propositions about propositions about 2‑dimensional universes of discourse. The early entries in their standard ordering define universes too amorphous to detain us for long on a first pass but as we turn toward the high end of the ordering we begin to recognize familiar structures worth examining from new angles.
present a formidable array of propositions about propositions about 2‑dimensional universes of discourse. The early entries in their standard ordering define universes too amorphous to detain us for long on a first pass but as we turn toward the high end of the ordering we begin to recognize familiar structures worth examining from new angles.
Instrumental to our study we define a couple of higher order operators,
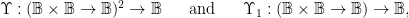
referred to as the relative and absolute umpire operators, respectively. If either operator is defined in terms of more primitive notions then the remaining operator can be defined in terms of the one first established.
Let 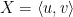 be a two‑dimensional boolean space,
be a two‑dimensional boolean space, 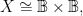 generated by two boolean variables or logical features
generated by two boolean variables or logical features  and
and 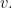
Given an ordered pair of propositions 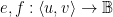 as arguments, the relative umpire operator reports the value
as arguments, the relative umpire operator reports the value  if the first implies the second, otherwise it reports the value
if the first implies the second, otherwise it reports the value 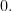

Expressing it another way:

In writing this, however, it is important to observe that the  appearing on the left side and the
appearing on the left side and the  appearing on the right side of the logical equivalence have different meanings. Filling in the details, we have the following.
appearing on the right side of the logical equivalence have different meanings. Filling in the details, we have the following.

Writing types as subscripts and using the fact that  it is possible to express this more succinctly as follows.
it is possible to express this more succinctly as follows.
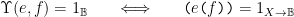
Finally, it is often convenient to write the first argument as a subscript. Thus we have the following equation.

The absolute umpire operator, also known as the umpire measure, is a higher order proposition  defined by the equation
defined by the equation  In this case the subscript
In this case the subscript  on the left and the argument
on the left and the argument  on the right both refer to the constant proposition
on the right both refer to the constant proposition  In most settings where
In most settings where  is applied to arguments it is safe to omit the subscript
is applied to arguments it is safe to omit the subscript  since the number of arguments indicates which type of operator is meant. Thus, we have the following identities and equivalents.
since the number of arguments indicates which type of operator is meant. Thus, we have the following identities and equivalents.

The umpire measure  is defined on boolean functions regarded as mathematical objects but can also be understood in terms of the judgments it induces on the syntactic level. In that interpretation
is defined on boolean functions regarded as mathematical objects but can also be understood in terms of the judgments it induces on the syntactic level. In that interpretation  recognizes theorems of the propositional calculus over
recognizes theorems of the propositional calculus over ![[u, v],](https://s0.wp.com/latex.php?latex=%5Bu%2C+v%5D%2C&bg=ffffff&fg=000000&s=0&c=20201002) giving a score of
giving a score of  to tautologies and a score of
to tautologies and a score of  to everything else, counting all contingent statements as no better than falsehoods.
to everything else, counting all contingent statements as no better than falsehoods.
One remark in passing for those who might prefer an alternative definition. If we had originally taken  to mean the absolute measure then the relative measure could have been defined as
to mean the absolute measure then the relative measure could have been defined as 
Resources
cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
whenever I ran across it. I suppose that small arc of revolution had been building for years but it struck me as crossing a threshold to a more explicit, self‑conscious stage about that time.