Inquiry Into Inquiry

Operator Variables in Logical Graphs • 10

Posted on April 18, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 9

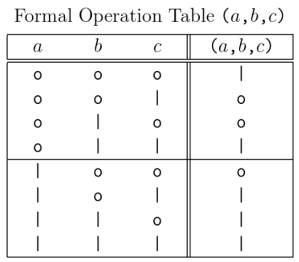
Let’s examine the Formal Operation Table for the third in our series of reflective forms to see if we can elicit the general pattern.

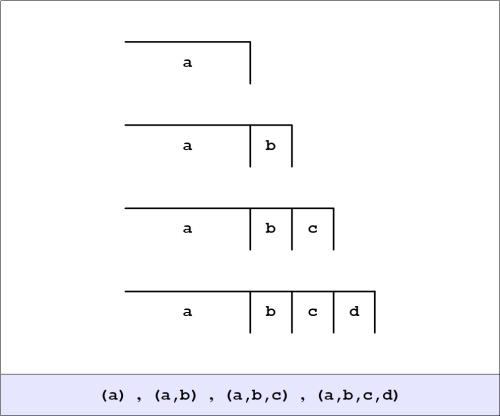
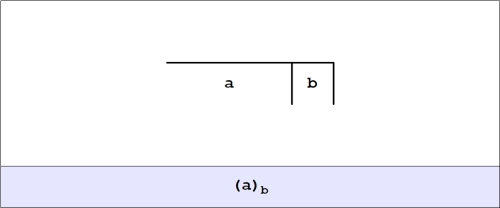
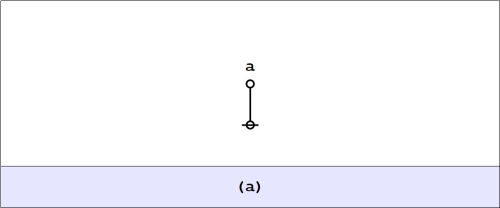
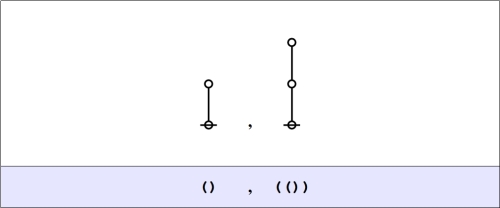
Alternatively, if we think in terms of the corresponding cactus graphs, writing ${}^{\backprime\backprime} \texttt{o} {}^{\prime\prime}$ for an unmarked node and ${}^{\backprime\backprime} \texttt{|} {}^{\prime\prime}$ for a terminal edge, we get the following Table.

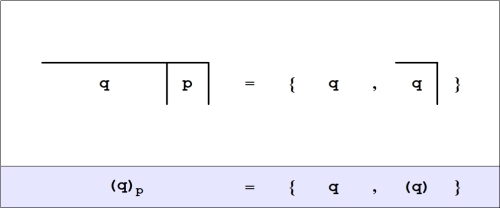
Evidently, the rule is that ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{)} {}^{\prime\prime}$ denotes the value denoted by ${}^{\backprime\backprime} \texttt{o} {}^{\prime\prime}$ if and only if exactly one of the variables $a, b, c$ has the value denoted by ${}^{\backprime\backprime} \texttt{|} {}^{\prime\prime},$ otherwise ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{)} {}^{\prime\prime}$ denotes the value denoted by ${}^{\backprime\backprime} \texttt{|} {}^{\prime\prime}.$ Examining the whole series of reflective forms shows this to be the general rule.

In the Entitative Interpretation $(\mathrm{En}),$ where $\texttt{o}$ = false and $\texttt{|}$ = true,
${}^{\backprime\backprime} \texttt{(} x_1 \texttt{,} \ldots \texttt{,} x_k \texttt{)} {}^{\prime\prime}$ translates as “not just one of the $x_j$ is true”.

In the Existential Interpretation $(\mathrm{Ex}),$ where $\texttt{o}$ = true and $\texttt{|}$ = false,
${}^{\backprime\backprime} \texttt{(} x_1 \texttt{,} \ldots \texttt{,} x_k \texttt{)} {}^{\prime\prime}$ translates as “just one of the $x_j$ is not true”.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 4 Comments

Operator Variables in Logical Graphs • 9

Posted on April 17, 2024 by Jon Awbrey

The following Table will suffice to show how the “streamer‑cross” forms C.S. Peirce used in his essay on “Qualitative Logic” and Spencer Brown used in his Laws of Form, as they are extended through successive steps of controlled reflection, translate into syntactic strings and rooted cactus graphs.

$\text{Syntactic Correspondences}$

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • 8

Posted on April 16, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 7

A trick of discovery I learned by observing Peirce’s working methods, more than anything he wrote outright, might be put in the following words.

Take what is constant, Treat it as variable, See if anything remains the same.

The step of controlled reflection we took with the previous post can be repeated at will, as suggested by the following series of forms.

Written inline, we have the series ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime},$ ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{)} {}^{\prime\prime},$ ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{)} {}^{\prime\prime},$ ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{,} d \texttt{)} {}^{\prime\prime},$ and so on, whose general form is ${}^{\backprime\backprime} \texttt{(} x_1 \texttt{,} x_2 \texttt{,} \ldots \texttt{,} x_k \texttt{)} {}^{\prime\prime}.$ With this move we have passed beyond the graph-theoretical form of rooted trees to what graph theorists know as rooted cacti.

I will discuss this cactus language and its logical interpretations next.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • 7

Posted on April 15, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 6

A funny thing just happened. Let’s see if we can tell where. We started with the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime},$ where the operand ${}^{\backprime\backprime} a {}^{\prime\prime}$ suggests the contemplated absence or presence of an arbitrary arithmetic expression. Next we contemplated the absence or presence of the operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ in ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}$ to be determined by the value of a newly introduced variable, say ${}^{\backprime\backprime} b {}^{\prime\prime},$ which is placed in a new slot of a newly extended operator form, as suggested by the following Figure.

What happened here is this. Our contemplation of a constant operator as being potentially variable gave rise to the contemplation of a newly introduced but otherwise quite ordinary operand variable, albeit in a newly-fashioned formula. In its interpretation for logic the newly formed operation may be viewed as an extension of ordinary negation, one in which the negation of the first variable is controlled by the value of the second variable.

We may regard this development as marking a form of controlled reflection, or a form of reflective control. From here on out we’ll use the inline syntax ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{)} {}^{\prime\prime}$ to indicate the corresponding operation on two variables, whose formal operation table is given below.

The Entitative Interpretation $(\mathrm{En}),$ for which $\texttt{Space} = \texttt{False}$ and $\texttt{Cross} = \texttt{True},$
calls this operation logical equality.
The Existential Interpretation $(\mathrm{Ex}),$ for which $\texttt{Space} = \texttt{True}$ and $\texttt{Cross} = \texttt{False},$
calls this operation logical difference.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • 6

Posted on April 14, 2024 by Jon Awbrey

Another tactic I tried by way of porting operator variables into Peirce’s logical graphs and Spencer Brown’s logical forms was to hollow out a leg of the latter’s crosses, gnomons, or markers, whatever you wish to call them, as shown below.

$Transitional Form (q)_p = {q,(q)}$

The initial idea I had in mind was the same as before, that the operator over $q$ would be counted as absent when $p$ evaluates to a space and present when $p$ evaluates to a cross.

However, much in the same way operators with a shade of negativity tend to be more generative than the purely positive brand, it turned out more useful to reverse the initial polarity of operation, letting the operator over $q$ be counted as absent when $p$ evaluates to a cross and present when $p$ evaluates to a space.

So that is the convention I’ll adopt from this point on.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • 5

Posted on April 12, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 4

We have encountered the question of how to extend our formal calculus to take account of operator variables.

In the days when I scribbled my logical graphs on the backs of computer punchcards, the first thing I tried was drawing big loopy script characters, placing some inside the loops of others. Lower case alphas, betas, gammas, deltas, and so on worked best. Graphs like that conveyed the idea that a character-shaped boundary drawn around an enclosed space can be viewed as absent or present depending on whether the formal value of the character in question is unmarked or marked. The same idea can be conveyed by attaching characters directly to the edges of graphs.

For example, the next Figure shows how we might suggest an algebraic expression of the form ${}^{\backprime\backprime} \texttt{(} q \texttt{)} {}^{\prime\prime}$ where the absence or presence of the operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ depends on the value of the algebraic expression ${}^{\backprime\backprime} p {}^{\prime\prime},$ the operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ being absent whenever $p$ is unmarked and present whenever $p$ is marked.

$Cactus Graph (q)_p = {q,(q)}$

It was clear from the outset that this sort of tactic would need a lot of work to become a usable calculus, especially when it came time to feed those punchcards back into the computer.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • 4

Posted on April 11, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 3

Last time we contemplated the penultimately simple algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}$ as a name for a set of arithmetic expressions, specifically, $\texttt{(} a \texttt{)} = \{ \,\texttt{()}\, , \,\texttt{(())}\, \},$ taking the equal sign in the appropriate sense.

Then we asked the corresponding question about the operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}.$ The above set of arithmetic expressions is what it means to contemplate the absence or presence of the arithmetic constant ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ in the place of the operand ${}^{\backprime\backprime} a {}^{\prime\prime}$ in the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}.$ But what would it mean to contemplate the absence or presence of the operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ in the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}?$

Evidently, a variation between the absence and the presence of the operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ in the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}$ refers to a variation between the algebraic expression ${}^{\backprime\backprime} a {}^{\prime\prime}$ and the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime},$ somewhat as pictured below.

But how shall we signify such variations in a coherent calculus?

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • 3

Posted on April 10, 2024 by Jon Awbrey

And if he is told that something is the way it is, then he thinks: Well, it could probably just as easily be some other way. So the sense of possibility might be defined outright as the capacity to think how everything could “just as easily” be, and to attach no more importance to what is than to what is not.

— Robert Musil • The Man Without Qualities

To get a clearer view of the relation between primary arithmetic and primary algebra consider the following extremely simple algebraic expression.

Here we see the variable name ${}^{\backprime\backprime} a {}^{\prime\prime}$ appearing as an operand name in the expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}.$ In functional terms, ${}^{\backprime\backprime} a {}^{\prime\prime}$ is called an argument name but it’s best to avoid the potentially confusing connotations of the word argument here, since it also refers in logical discussions to a more or less specific pattern of reasoning.

In effect, the algebraic variable name indicates the contemplated absence or presence of any arithmetic expression taking its place in the surrounding template, which expression is proxied well enough by its formal value, and of which values we know but two. Putting it all together, the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}$ varies between the following two choices.

The above set of arithmetic expressions is what it means to contemplate the absence or presence of the arithmetic constant ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ in the place of the operand ${}^{\backprime\backprime} a {}^{\prime\prime}$ in the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}.$ But what would it mean to contemplate the absence or presence of the operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ in the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}?$

That is the question I’ll take up next.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • Discussion 2

Posted on April 9, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 1
Re: Cybernetics List • Lou Kauffman

LK:

I am writing to comment that there are some quite interesting situations that generalize the De Morgan Duality.

One well-known one is this. Let $\mathbb{R}^*$ denote the real numbers with a formal symbol $@,$ denoting infinity, adjoined so that:

$\begin{array}{cccccl} @ & + & @ & = & @ & \\ @ & + & 0 & = & @ & \\ @ & + & x & = & @ & \text{when}~ x ~\text{is an ordinary real number} \\ 1 & \div & @ & = & 0 \end{array}$

(Of course you cannot do anything with $@$ or the system collapses. One can easily give the constraints.)

Define $\lnot x = 1/x.$

$x + y = \text{usual sum otherwise.}$

Define $x * y = xy/(x+y) = 1/((1/x) + (1/y)).$

Then we have $x*y = \lnot (\lnot x + \lnot y),$ so that the system $(\mathbb{R}^*, \lnot, +, *)$ satisfies De Morgan duality and it is a Boolean algebra when restricted to $\{ 0, @ \}.$

Note also that $\lnot$ fixes $1$ and $-1.$ This algebraic system occurs of course in electrical calculations and also in the properties of tangles in knot theory, as you can read in the last part of my included paper “Knot Logic”. I expect there is quite a bit more about this kind of duality in various (categorical) places.

Thanks, Lou, there’s a lot to think about here, so I’ll need to study it a while. Just off hand, the embedding into reals brings up a vague memory of the very curious way Peirce defines negation in his 1870 “Logic of Relatives”. I seem to recall it involving a power series, but it’s been a while so I’ll have to look it up again.

Regards,

Jon

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • Discussion 1

Posted on April 8, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 1
Re: Academia.edu • Stephen Duplantier

SD:: The best way for me to read Peirce is as if he was writing poetry. So if his algebra is poetry — I imagine him approving of the approach since he taught me abduction in the first place — there is room to wander. With this, I venture the idea that his “wide field” is a local algebraic geography far from the tended garden. There, where weeds and wild things grow and hybridize are the non‑dichotomic mathematics.

“Abdeuces Are Wild”, as they say, maybe not today, maybe not tomorrow, but soon …

As far as my own guess, and a lot of my wandering in pursuit of it goes, I’d venture Peirce’s field of vision opens up not so much from dichotomic to trichotomic domains of value as from dyadic to triadic relations, and all that with particular significance into the medium of reflection afforded by triadic sign relations.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

	Survey of Semiotics,… on Sign Relations • Graphical…
	Sign Relations • Gra… on Survey of Semiotics, Semiosis,…
	Survey of Semiotics,… on Sign Relations • Graphical…
	Sign Relations • Gra… on Survey of Semiotics, Semiosis,…
	Jon Awbrey on Sign Relations • Definiti…
	Jon Awbrey on Sign Relations • Definiti…
	Jon Awbrey on Sign Relations • Definiti…
	Survey of Semiotics,… on Sign Relations • Semiotic Equi…
	Survey of Semiotics,… on Sign Relations • Semiotic Equi…
	Sign Relations • Sem… on Survey of Semiotics, Semiosis,…

M	T	W	T	F	S	S
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

Inquiry Into Inquiry

Operator Variables in Logical Graphs • 10

Operator Variables in Logical Graphs • 9

Operator Variables in Logical Graphs • 8

Operator Variables in Logical Graphs • 7

Operator Variables in Logical Graphs • 6

Operator Variables in Logical Graphs • 5

Operator Variables in Logical Graphs • 4

Operator Variables in Logical Graphs • 3

Operator Variables in Logical Graphs • Discussion 2

Operator Variables in Logical Graphs • Discussion 1

Resources

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Inquiry Driven Systems

Cybernetics

Differential Logic

Logical Graphs

Minimal Negation Operators

Peirce Matters

Relation Theory

Riffs & Rotes

Semeiotics

Theme One

Current Events

Fawkes News

Meta

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Resources

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta