From Dyadic to Triadic to Sign Relations
Peirce’s notation for elementary relatives was illustrated earlier by a dyadic relation from number theory, namely, the relation written for
Cf: Relations & Their Relatives • 3
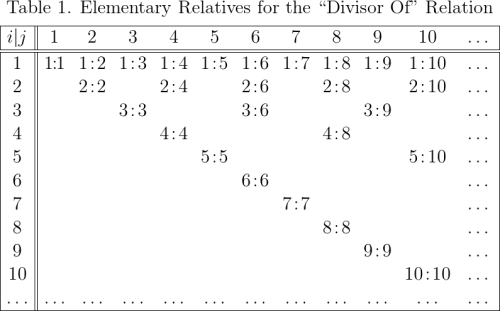
Table 1 shows the first few ordered pairs of the relation on positive integers corresponding to the relative term, “divisor of”. Thus, the ordered pair appears in the relation if and only if
divides
for which the usual mathematical notation is
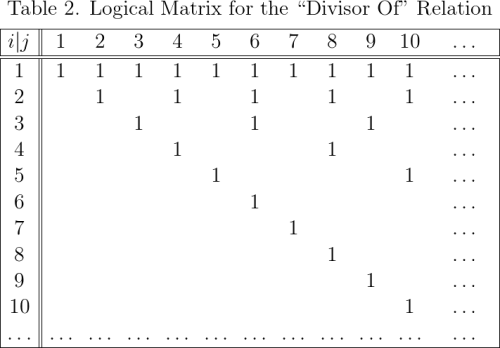
Table 2 shows the same information in the form of a logical matrix. This has a coefficient of in row
and column
when
otherwise it has a coefficient of
(The zero entries have been omitted for ease of reading.)
Just as matrices of real coefficients in linear algebra represent linear transformations, matrices of boolean coefficients represent logical transformations. The capacity of dyadic relations to generate transformations gives us part of what we need to know about the dynamics of semiosis inherent in sign relations.
Cf: Relations & Their Relatives • Discussion 1
The “divisor of” relation is a dyadic relation on the set of positive integers
and thus may be understood as a subset of the cartesian product
It forms an example of a partial order relation, while the “less than or equal to” relation
is an example of a total order relation.
The mathematics of relations can be applied most felicitously to semiotics but there we must bump the adicity or arity up to three. We take any sign relation to be subset of a cartesian product
where
is the set of objects under consideration in a given discussion,
is the set of signs, and
is the set of interpretant signs involved in the same discussion.
One thing we need to understand is the sign relation relevant to a given level of discussion may be rather more abstract than what we would call a sign process proper, that is, a structure extended through a dimension of time. Indeed, many of the most powerful sign relations generate sign processes through iteration or recursion or similar operations. In that event, the most penetrating analysis of the sign process or semiosis in view is achieved through grasping the generative sign relation at its core.
Resources
cc: Category Theory • Cybernetics • Ontolog • Structural Modeling • Systems Science
cc: FB | Relation Theory • Laws of Form • Peirce List (1) (2) (3)

Pingback: Survey of Relation Theory • 4 | Inquiry Into Inquiry
Pingback: Relations & Their Relatives • Discussion 18 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 5 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 2 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 3 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 6 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 7 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 8 | Inquiry Into Inquiry