Animated Logical Graphs • 75

Posted on May 10, 2021 by Jon Awbrey

Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (30) • (45) • (57) • (58) • (59) • (60) • (61) • (62) • (63) • (64) • (65) • (66) • (69) • (70) • (71) • (72) • (73) • (74)

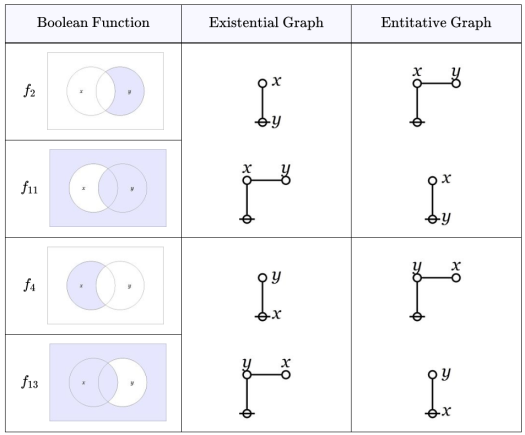
Continuing our scan of the Table in Episode 72, the next two orbits contain the logical graphs for the boolean functions f_{2}, f_{11}, f_{4}, f_{13}, in that order.  A first glance shows these two orbits have surprisingly intricate structures and relationships to each other — let’s isolate that section for a closer look.

\text{Peirce Duality} \stackrel{_\bullet}{} \text{Subtractions and Implications}

Peirce Duality • Subtractions and Implications

  • The boolean functions f_{2} and f_{4} are called subtraction functions.
  • The boolean functions f_{11} and f_{13} are called implication functions.
  • The logical graphs for f_{2} and f_{11} are dual to each other.
  • The logical graphs for f_{4} and f_{13} are dual to each other.

The values of the subtraction and implication functions for each (x, y) \in \mathbb{B} \times \mathbb{B} and the text expressions for their logical graphs are given in the following Table.

Subtractions and Implications

Resources

cc: Peirce List (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: FB | Logical Graphs • Laws of Form

This entry was posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization and tagged , , , , , , , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.

2 Responses to Animated Logical Graphs • 75

  1. Pingback: Survey of Animated Logical Graphs • 4 | Inquiry Into Inquiry

  2. Pingback: Animated Logical Graphs • 76 | Inquiry Into Inquiry

Leave a Reply

Fill in your details below or click an icon to log in:

Gravatar
WordPress.com Logo

You are commenting using your WordPress.com account. ( Log Out /  Change )

Twitter picture

You are commenting using your Twitter account. ( Log Out /  Change )

Facebook photo

You are commenting using your Facebook account. ( Log Out /  Change )

Cancel

Connecting to %s

This site uses Akismet to reduce spam. Learn how your comment data is processed.