Animated Logical Graphs • 50

Posted on December 5, 2020 by Jon Awbrey

Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (30) (45) (46) (47) (48) (49)

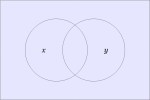
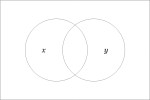
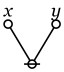
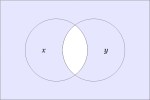
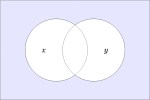
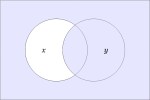
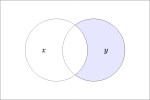
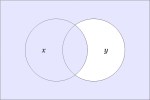
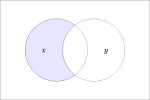
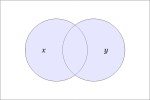
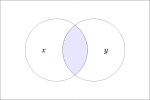
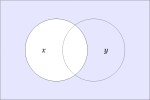
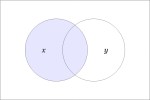
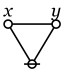
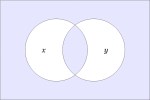
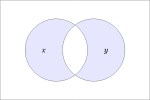
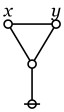
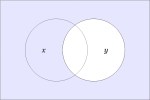
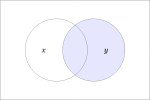
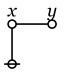
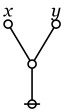
In the last of our six ways of looking at the Peirce duality between entitative and existential interpretations, we consider the previous Table of Logical Graphs and Venn Diagrams sorted in Orbit Order.

Logical Graphs • Entitative and Existential Venn Diagrams • Orbit Order
\text{Logical Graph} \text{Entitative Interpretation} \text{Existential Interpretation}
Cactus Stem
 		 f₁₅(x,y) f₀(x,y)
\texttt{(} ~ \texttt{)}
 		 \text{true}
f_{15}		 \text{false}
f_{0}
Cactus (x)(y)
 		 f₇(x,y) f₁(x,y)
\texttt{(} x \texttt{)(} y \texttt{)}
 		 \lnot x \lor \lnot y
f_{7}		 \lnot x \land \lnot y
f_{1}
Cactus (x)y
 		 f₁₁(x,y) f₂(x,y)
\texttt{(} x \texttt{)} y
 		 x \Rightarrow y
f_{11}		 x \nLeftarrow y
f_{2}
Cactus x(y)
 		 f₁₃(x,y) f₄(x,y)
x \texttt{(} y \texttt{)}
 		 x \Leftarrow y
f_{13}		 x \nRightarrow y
f_{4}
Cactus xy
 		 f₁₄(x,y) f₈(x,y)
x y
 		 x \lor y
f_{14}		 x \land y
f_{8}
Cactus (x)
 		 f₃(x,y) f₃(x,y)
\texttt{(} x \texttt{)}
 		 \lnot x
f_{3}		 \lnot x
f_{3}
Cactus x
 		 f₁₂(x,y) f₁₂(x,y)
x
 		 x
f_{12}		 x
f_{12}
Cactus (x,y)
 		 f₉(x,y) f₆(x,y)
\texttt{(} x \texttt{,} y \texttt{)}
 		 x = y
f_{9}		 x \ne y
f_{6}
Cactus ((x,y))
 		 f₆(x,y) f₉(x,y)
\texttt{((} x \texttt{,} y \texttt{))}
 		 x \ne y
f_{6}		 x = y
f_{9}
Cactus (y)
 		 f₅(x,y) f₅(x,y)
\texttt{(} y \texttt{)}
 		 \lnot y
f_{5}		 \lnot y
f_{5}
Cactus y
 		 f₁₀(x,y) f₁₀(x,y)
y
 		 y
f_{10}		 y
f_{10}
Cactus (xy)
 		 f₁(x,y) f₇(x,y)
\texttt{(} x y \texttt{)}
 		 \lnot (x \lor y)
f_{1}		 \lnot (x \land y)
f_{7}
Cactus (x(y))
 		 f₂(x,y) f₁₁(x,y)
\texttt{(} x \texttt{(} y \texttt{))}
 		 x \nLeftarrow y
f_{2}		 x \Rightarrow y
f_{11}
Cactus ((x)y)
 		 f₄(x,y) f₁₃(x,y)
\texttt{((} x \texttt{)} y \texttt{)}
 		 x \nRightarrow y
f_{4}		 x \Leftarrow y
f_{13}
Cactus ((x)(y))
 		 f₈(x,y) f₁₄(x,y)
\texttt{((} x \texttt{)(} y \texttt{))}
 		 x \land y
f_{8}		 x \lor y
f_{14}
Cactus Root
 		 f₀(x,y) f₁₅(x,y)
 
 		 \text{false}
f_{0}		 \text{true}
f_{15}

Resources

cc: Cybernetics Communications (1) (2) • FB | Logical Graphs • Ontolog Forum (1) (2)
cc: Peirce (1) (2) (3) (4) (5) (6) (7) (8) (9) • Structural Modeling (1) (2) • Systems (1) (2)

This entry was posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization and tagged , , , , , , , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.

3 Responses to Animated Logical Graphs • 50

  1. Pingback: Survey of Animated Logical Graphs • 3 | Inquiry Into Inquiry

  2. Pingback: Survey of Animated Logical Graphs • 4 | Inquiry Into Inquiry

  3. Pingback: Survey of Animated Logical Graphs • 5 | Inquiry Into Inquiry

Leave a Reply

Fill in your details below or click an icon to log in:

Gravatar
WordPress.com Logo

You are commenting using your WordPress.com account. ( Log Out /  Change )

Facebook photo

You are commenting using your Facebook account. ( Log Out /  Change )

Cancel

Connecting to %s

This site uses Akismet to reduce spam. Learn how your comment data is processed.