Semiotic Transformations

Re: Transformations of Logical Graphs • (8) • (9) • (10) • (11)
Re: Interpretive Duality as Sign Relation • Orbit Order

Taking from our wallets an old schedule of orbits, let’s review the classes of logical graphs we’ve covered so far.

Self-Dual Logical Graphs

Four orbits of self‑dual logical graphs, were discussed in Episode 9.

The logical graphs denote the boolean functions in that order.  The value of each function at each point in is shown in the Table above.

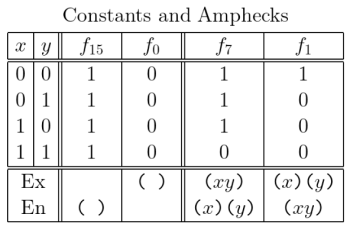
Constants and Amphecks

Two orbits of logical graphs called constants and amphecks were discussed in Episode 10.

The constant logical graphs denote the constant functions

• Under the logical graph whose text form is “  ” denotes the function
  and the logical graph whose text form is denotes the function
• Under the logical graph whose text form is “  ” denotes the function
  and the logical graph whose text form is denotes the function

The ampheck logical graphs denote the ampheck functions

• Under the logical graph denotes the function
  and the logical graph denotes the function
• Under the logical graph denotes the function
  and the logical graph denotes the function

Subtractions and Implications

The logical graphs called subtractions and implications were discussed in Episode 11.

The subtraction logical graphs denote the subtraction functions

The implication logical graphs denote the implication functions

Under the action of the duality the logical graphs for the subtraction and the implication fall into one orbit while the logical graphs for the subtraction and the implication fall into another orbit, making these two partitions of the four functions orthogonal or transversal to each other.

Resources

• Logic Syllabus
• Logical Graphs • Zeroth Order Logic
• Survey of Animated Logical Graphs
• Survey of Semiotics, Semiosis, Sign Relations

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science