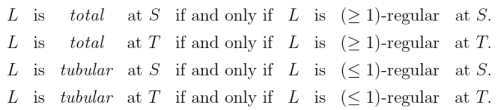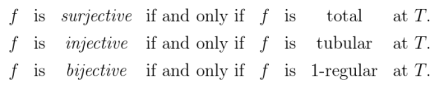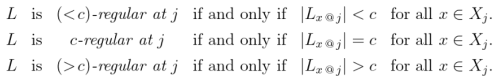Inquiry Into Inquiry

Relation Theory • 6

Posted on November 4, 2021 by Jon Awbrey

Relation Theory • Species of Dyadic Relations

Returning to 2‑adic relations, it is useful to describe several familiar classes of objects in terms of their local and numerical incidence properties. Let $L \subseteq S \times T$ be an arbitrary 2‑adic relation. The following properties of $L$ can be defined.

If $L \subseteq S \times T$ is tubular at $S$ then $L$ is called a partial function or a prefunction from $S$ to $T.$ This is sometimes indicated by giving $L$ an alternate name, for example, ${}^{\backprime\backprime} p {}^{\prime\prime},$ and writing $L = p : S \rightharpoonup T.$ Thus we have the following definition.

$\begin{matrix} L & = & p : S \rightharpoonup T & \text{if and only if} & L & \text{is} & \text{tubular} & \text{at}~ S. \end{matrix}$

If $L$ is a prefunction $p : S \rightharpoonup T$ which happens to be total at $S,$ then $L$ is called a function from $S$ to $T,$ indicated by writing $L = f : S \to T.$ To say a relation $L \subseteq S \times T$ is totally tubular at $S$ is to say it is $1$ -regular at $S.$ Thus, we may formalize the following definition.

$\begin{matrix} L & = & f : S \to T & \text{if and only if} & L & \text{is} & 1\text{-regular} & \text{at}~ S. \end{matrix}$

In the case of a function $f : S \to T,$ we have the following additional definitions.

Resources

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Relation Theory • Laws of Form • Peirce List

Posted in C.S. Peirce, Category Theory, Dyadic Relations, Logic, Logic of Relatives, Logical Graphs, Mathematics, Nominalism, Peirce, Pragmatism, Realism, Relation Theory, Semiotics, Sign Relations, Triadic Relations, Visualization | Tagged C.S. Peirce, Category Theory, Dyadic Relations, Logic, Logic of Relatives, Logical Graphs, Mathematics, Nominalism, Peirce, Pragmatism, Realism, Relation Theory, Semiotics, Sign Relations, Triadic Relations, Visualization | 9 Comments

Relation Theory • Discussion 3

Posted on November 3, 2021 by Jon Awbrey

Re: Relation Theory • (1) • (2) • (3) • (4) • (5)
Re: Laws of Form • James Bowery

JB:

Thanks for that very rigorous definition of “relation theory”.

Its “trick” of including the name of the $k$ -relation in a $(k+1)$ -relation’s tuples reminds me Etter’s paper “Three-Place Identity” which was the result of some of our work at HP on dealing with identity (starting with the very practical need to identify individuals/corporations, etc. for the purpose of permitting meta-data that attributed assertions of fact to certain identities aka “provenance” of data).

The result of that effort threatens to up-end set theory itself and was to be fully fleshed out in “Membership and Identity” […]

We were able to get a preliminary review of Three-Place Identity by a close associate of Ray Smullyan. It came back with a positive verdict. I believe I may still have that letter somewhere in my archives.

Dear James,

The article on Relation Theory represents my attempt to bridge the two cultures of weak typing and strong typing approaches to functions and relations. Weak typing was taught in those halcyon Halmos days when functions and relations were nothing but subsets of cartesian products. Strong typing came to the fore with category theory, its arrows from source to target domains, and the need for closely watched domains in computer science.

Peirce recognizes a fundamental triadic relation he calls “teridentity” where three variables $a, b, c$ denote the same object, represented in his logical graphs as a node of degree three, and at first I thought you might be talking about that.

But I see $x(y = z)$ read as ${}^{\backprime\backprime} x ~\text{regards}~ y ~\text{as the same as}~ z {}^{\prime\prime}$ is more like the expressions I use to discuss “equivalence relations from a particular point of view”, following one of Peirce’s more radical innovations from his 1870 “Logic of Relatives”.

C.S. Peirce • On the Doctrine of Individuals (1) (2)

Using square brackets in the form $[a]_e$ for the equivalence class of an element $a$ in an equivalence relation $e$ we can express the above idea in one of the following forms.

$\begin{matrix} [y = z]_x & \text{or} & [y]_x = [z]_x & \text{or} & y =_x z \end{matrix}$

I wrote this up in general somewhere but there’s a fair enough illustration of the main idea in the following application to “semiotic equivalence relations”.

Semiotic Equivalence Relations • (1) (2)

The rest of your remarks bring up a wealth of associations for me, as seeing the triadic unity in the multiplicity of dyadic appearances is a lot of what the Peircean perspective is all about. I’ll have to dig up a few old links to fill that out …

Regards,

Jon

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Relation Theory • Laws of Form • Peirce List

Posted in Algebra, Algebra of Logic, C.S. Peirce, Category Theory, Combinatorics, Discrete Mathematics, Duality, Dyadic Relations, Foundations of Mathematics, Graph Theory, Logic, Logic of Relatives, Mathematics, Peirce, Relation Theory, Semiotics, Set Theory, Sign Relational Manifolds, Sign Relations, Triadic Relations, Type Theory, Visualization | Tagged Algebra, Algebra of Logic, C.S. Peirce, Category Theory, Combinatorics, Discrete Mathematics, Duality, Dyadic Relations, Foundations of Mathematics, Graph Theory, Logic, Logic of Relatives, Mathematics, Peirce, Relation Theory, Semiotics, Set Theory, Sign Relational Manifolds, Sign Relations, Triadic Relations, Type Theory, Visualization | 9 Comments

Relation Theory • Discussion 2

Posted on November 1, 2021 by Jon Awbrey

Re: Relation Theory • (1) • (2) • (3) • (4)
Re: FB | Charles S. Peirce Society • Joseph Harry

JH:: These are iconic representations dealing with logical symbolic relations, and so of course are semiotic in Peirce’s sense, since logic is semiotic. But couldn’t a logician do all of this meticulous formalization and understand all of the discrete logical consequences of it without having any inkling of semiotics or of Peirce?

Dear Joseph,

As I noted at the top of the article and blog series —

This article treats relations from the perspective of combinatorics, in other words, as a subject matter in discrete mathematics, with special attention to finite structures and concrete set-theoretic constructions, many of which arise quite naturally in applications. This approach to relation theory, or the theory of relations, is distinguished from, though closely related to, its study from the perspectives of abstract algebra on the one hand and formal logic on the other.

Of course one can always pull a logical formalism out of thin air, with no inkling of its historical sources, and proceed in a blithely syntactic and deductive fashion. But if we hew more closely to applications, original or potential, and even regard logic and math as springing from practice, we must take care for the semantic and pragmatic grounds of their use. From that perspective, models come first, well before the deductive theories whose consistency they establish.

Regards,

Jon

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Relation Theory • Laws of Form • Peirce List

Relation Theory • 5

Posted on October 31, 2021 by Jon Awbrey

Relation Theory

Two further classes of incidence properties will prove to be of great utility.

Regional Incidence Properties

The definition of a local flag can be broadened from a point to a subset of a relational domain, arriving at the definition of a regional flag in the following way.

Let $L$ be a $k$ -place relation $L \subseteq X_1 \times \ldots \times X_k.$

Choose a relational domain $X_j$ and a subset $M \subseteq X_j.$

Then $L_{M\,@\,j}$ is a subset of $L$ called the flag of $L$ with $M$ at $j,$ or the $(M\,@\,j)$ -flag of $L,$ a mathematical object with the following definition.

$L_{M\,@\,j} ~ = ~ \{ (x_1, \ldots, x_j, \ldots, x_k) \in L ~ : ~ x_j \in M \}.$

Numerical Incidence Properties

A numerical incidence property of a relation is a local incidence property predicated on the cardinalities of its local flags.

For example, $L$ is said to be $c$ -regular at $j$ if and only if the cardinality of the local flag $L_{x\,@\,j}$ is $c$ for all $x$ in ${X_j}$ — to write it in symbols, if and only if $|L_{x\,@\,j}| = c$ for all ${x \in X_j}.$

In a similar fashion, one may define the numerical incidence properties, $(<\!c)$ -regular at $j,$ $(>\!c)$ -regular at $j,$ and so on. For ease of reference, a few definitions are recorded below.

Resources

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Relation Theory • Laws of Form • Peirce List

Relation Theory • 4

Posted on October 30, 2021 by Jon Awbrey

Relation Theory • Local Incidence Properties

The next few definitions of local incidence properties of relations are given at a moderate level of generality in order to show how they apply to $k$ -place relations. In the sequel we’ll see what light they throw on a number of more familiar two-place relations and functions.

A local incidence property of a relation $L$ is a property which depends in turn on the properties of special subsets of $L$ known as its local flags. The local flags of a relation are defined in the following way.

Let $L$ be a $k$ -place relation $L \subseteq X_1 \times \ldots \times X_k.$

Select a relational domain ${X_j}$ and one of its elements $x.$

Then $L_{x\,@\,j}$ is a subset of $L$ called the flag of $L$ with $x$ at $j,$ or the $(x\,@\,j)$ -flag of $L,$ a mathematical object with the following definition.

$L_{x\,@\,j} ~ = ~ \{ (x_1, \ldots, x_j, \ldots, x_k) \in L ~ : ~ x_j = x \}.$

Any property $C$ of the local flag $L_{x\,@\,j}$ is said to be a local incidence property of $L$ with respect to the locus $x\,@\,j.$

A $k$ -adic relation $L \subseteq X_1 \times \ldots \times X_k$ is said to be $C$ -regular at $j$ if and only if every flag of $L$ with $x$ at $j$ has the property $C,$ where $x$ is taken to vary over the theme of the fixed domain $X_j.$

Expressed in symbols, $L$ is $C$ -regular at $j$ if and only if $C(L_{x\,@\,j})$ is true for all $x$ in $X_j.$

Resources

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Relation Theory • Laws of Form • Peirce List

Relation Theory • 3

Posted on October 29, 2021 by Jon Awbrey

Relation Theory • Definition

It is convenient to begin with the definition of a $k$ -place relation, where $k$ is a positive integer.

Definition. A $k$ -place relation $L \subseteq X_1 \times \ldots \times X_k$ over the nonempty sets $X_1, \ldots, X_k$ is
a $(k+1)$ -tuple $(X_1, \ldots, X_k, L)$ where $L$ is a subset of the cartesian product $X_1 \times \ldots \times X_k.$

Several items of terminology are useful in discussing relations.

The sets $X_1, \ldots, X_k$ are called the domains of the relation $L \subseteq X_1 \times \ldots \times X_k,$ with ${X_j}$ being the $j^\text{th}$ domain.

If all the ${X_j}$ are the same set $X$ then $L \subseteq X_1 \times \ldots \times X_k$ is more simply described as a
$k$ -place relation over $X.$

The set $L$ is called the graph of the relation $L \subseteq X_1 \times \ldots \times X_k,$ on analogy with the graph of a function.

If the sequence of sets $X_1, \ldots, X_k$ is constant throughout a given discussion or is otherwise determinate in context then the relation $L \subseteq X_1 \times \ldots \times X_k$ is determined by its graph $L,$ making it acceptable to denote the relation by referring to its graph.

Other synonyms for the adjective $k$ -place are $k$ -adic and $k$ -ary, all of which leads to the integer $k$ being called the dimension, adicity, or arity of the relation $L.$

Resources

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Relation Theory • Laws of Form • Peirce List

Relation Theory • 2

Posted on October 28, 2021 by Jon Awbrey

Relation Theory • Preliminaries

Two definitions of the relation concept are common in the literature. Although it is usually clear in context which definition is being used at a given time, it tends to become less clear as contexts collide, or as discussion moves from one context to another.

The same sort of ambiguity arose in the development of the function concept and it may save a measure of effort to follow the pattern of resolution that worked itself out there.

When we speak of a function $f : X \to Y$ we are thinking of a mathematical object whose articulation requires three pieces of data, specifying the set $X,$ the set $Y,$ and a particular subset of their cartesian product ${X \times Y}.$ So far so good.

Let us write $f = (\mathrm{obj_1}f, \mathrm{obj_2}f, \mathrm{obj_{12}}f)$ to express what has been said so far.

When it comes to parsing the notation ${}^{\backprime\backprime} f : X \to Y {}^{\prime\prime},$ everyone takes the part ${}^{\backprime\backprime} X \to Y {}^{\prime\prime}$ as indicating the type of the function, in effect defining $\mathrm{type}(f)$ as the pair $(\mathrm{obj_1}f, \mathrm{obj_2}f),$ but ${}^{\backprime\backprime} f {}^{\prime\prime}$ is used equivocally to denote both the triple $(\mathrm{obj_1}f, \mathrm{obj_2}f, \mathrm{obj_{12}}f)$ and the subset $\mathrm{obj_{12}}f$ forming one part of it.

One way to resolve the ambiguity is to formalize a distinction between the function $f = (\mathrm{obj_1}f, \mathrm{obj_2}f, \mathrm{obj_{12}}f)$ and its graph, defining $\mathrm{graph}(f) = \mathrm{obj_{12}}f.$

Another tactic treats the whole notation ${}^{\backprime\backprime} f : X \to Y {}^{\prime\prime}$ as a name for the triple, letting ${}^{\backprime\backprime} f {}^{\prime\prime}$ denote $\mathrm{graph}(f).$

In categorical and computational contexts, at least initially, the type is regarded as an essential attribute or integral part of the function itself. In other contexts we may wish to use a more abstract concept of function, treating a function as a mathematical object capable of being viewed under many different types.

Following the pattern of the functional case, let the notation ${}^{\backprime\backprime} L \subseteq X \times Y {}^{\prime\prime}$ bring to mind a mathematical object specified by three pieces of data, the set $X,$ the set $Y,$ and a particular subset of their cartesian product ${X \times Y}.$ As before we have two choices, either let $L$ be the triple $(X, Y, \mathrm{graph}(L))$ or let ${}^{\backprime\backprime} L {}^{\prime\prime}$ denote $\mathrm{graph}(L)$ and choose another name for the triple.

Resources

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Relation Theory • Laws of Form • Peirce List

Relation Theory • 1

Posted on October 27, 2021 by Jon Awbrey

Here’s an introduction to Relation Theory geared to applications and taking a moderately general view at least as far as finite numbers of relational domains are concerned ( $k$ -adic or $k$ -ary relations).

Relation Theory

This article treats relations from the perspective of combinatorics, in other words, as a subject matter in discrete mathematics, with special attention to finite structures and concrete set‑theoretic constructions, many of which arise quite naturally in applications. This approach to relation theory, or the theory of relations, is distinguished from, though closely related to, its study from the perspectives of abstract algebra on the one hand and formal logic on the other.

Resources

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Relation Theory • Laws of Form • Peirce List

Zeroth Law Of Semiotics • Discussion 1

Posted on October 26, 2021 by Jon Awbrey

Re: Zeroth Law Of Semiotics • Comment 2
Re: Laws of Form • John Mingers

JM:: Hmmm
Sounds terribly like analytic philosophy to me.
There are not real philosophical problems, it’s all just a matter of misuse of words.
Have you seen the world out there — there really are problems that philosophy ought to try and help with!!!

Dear John,

If I have a philosophy it would be pragmatism. A pragmatist — or pragmatician as I sometimes prefer — is more like a type of reflective practitioner, one who applies the pragmatic maxim to clarify ideas, all the better to apply ideas to pressing realities.

Pragmatic Maxim: The pragmatic maxim is a guideline for the practice of inquiry formulated by Charles Sanders Peirce. Serving as a normative recommendation or regulative principle in the normative science of logic, its function is to guide the conduct of thought toward the achievement of its aims, advising the addressee on an optimal way of “attaining clearness of apprehension”.

In pragmatic ways of thinking, semiotics is a discipline of critical reflection charged with sorting out the respective roles of signs, ideas, and objects (including objects in the sense of aims, ends, goals, objectives, and purposes) in the activities of communication, learning, and reasoning.

That is what I’m about here.

Regards,

Jon

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Semeiotics • Laws of Form (1) (2) • Peirce List (1) (2) (3)

Posted in C.S. Peirce, Denotation, Extension, Information = Comprehension × Extension, Liar Paradox, Logic, Nominalism, Peirce, Pragmatics, Rhetoric, Semantics, Semiositis, Semiotics, Sign Relations, Syntax, Zeroth Law Of Semiotics | Tagged C.S. Peirce, Denotation, Extension, Information = Comprehension × Extension, Liar Paradox, Logic, Nominalism, Peirce, Pragmatics, Rhetoric, Semantics, Semiositis, Semiotics, Sign Relations, Syntax, Zeroth Law Of Semiotics | 6 Comments

All Liar, No Paradox • Discussion 2

Posted on October 23, 2021 by Jon Awbrey

Re: Laws of Form • James Bowery • John Mingers

Dear James, John, et al.

The questions arising in the present discussion take us back to the question of what we are using logical values like $\textsc{true}$ and $\textsc{false}$ for, which takes us back to the question of what we are using our logical systems for.

One of the things we use logical values like $\textsc{true}$ and $\textsc{false}$ for is to mark the sides of a distinction we have drawn, or noticed, or maybe just think we see in a logical universe of discourse or space $X.$

This leads us to speak of logical functions $f : X \to \mathbb{B},$ where $\mathbb{B}$ is the so-called boolean domain $\mathbb{B} = \{ \textsc{false}, \textsc{true} \}.$ But we are really using $\mathbb{B}$ only “up to isomorphism”, as they say in the trade, meaning we are using it as a generic 2-point set and any other 1-bit set will do as well, like $\mathbb{B} = \{ 0, 1 \}$ or $\mathbb{B} = \{ \textsc{white}, \textsc{blue} \},$ my favorite colors for painting the areas of a venn diagram.

A function like $f : X \to \mathbb{B} = \{ 0, 1 \}$ is called a “characteristic function” in set theory since it characterizes a subset $S$ of $X$ where the value of $f$ is $1.$ But I like the language they use in statistics, where $f : X \to \mathbb{B}$ is called an “indicator function” since it indicates a subset of $X$ where $f$ evaluates to $1.$

The indicator function of a subset $S$ of $X$ is notated as $f_S : X \to \mathbb{B}$ and defined as the function $f_S : X \to \mathbb{B}$ where $f_S (x) = 1$ if and only if $x \in S.$ I like this because it links up nicely with the sense of indication in the calculus of indications.

The indication in question is the subset $S$ of $X$ indicated by the function $f_S : X \to \mathbb{B}.$ Other names for it are the “fiber” or “pre-image“ of $1.$ It is computed by way of the “inverse function” $f_S^{-1}$ in the rather ugly but pre-eminently useful way as $S = f_S^{-1}(1).$

Regards,

Jon

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Logical Graphs • Laws of Form • Peirce List

Posted in Bertrand Russell, C.S. Peirce, Epimenides, Laws of Form, Liar Paradox, Logic, Logical Graphs, Mathematics, Paradox, Pragmatics, Rhetoric, Semantics, Semiositis, Semiotics, Sign Relations, Spencer Brown, Syntax, Visualization | Tagged Bertrand Russell, C.S. Peirce, Epimenides, Laws of Form, Liar Paradox, Logic, Logical Graphs, Mathematics, Paradox, Pragmatics, Rhetoric, Semantics, Semiositis, Semiotics, Sign Relations, Spencer Brown, Syntax, Visualization | 6 Comments

	Survey of Differenti… on Differential Logic • 5
	Differential Logic •… on Differential Logic • 4
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Differential Logic •… on Differential Logic • 4
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 4

M	T	W	T	F	S	S
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28

Relation Theory • Species of Dyadic Relations

Resources

Share this:

Share this:

Share this:

Resources

Share this:

Relation Theory • Local Incidence Properties

Resources

Share this:

Relation Theory • Definition

Resources

Share this:

Relation Theory • Preliminaries

Resources

Share this:

Resources

Share this:

Share this:

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta