Inquiry Into Inquiry

Peircean Semiotics and Triadic Sign Relations • 2

Posted on August 22, 2024 by Jon Awbrey

When I returned to graduate school for the third time around, this time in systems engineering, I had in mind integrating my long‑standing projects investigating the dynamics of information, inquiry, learning, and reasoning, viewing each as a process whose trajectory evolves over time through the medium which gives it concrete embodiment, namely, a triadic sign relation.

Up until that time I don’t believe I’d ever given much thought to sign relations that had anything smaller than infinite domains of objects, signs, and interpretant signs. Countably infinite domains are what come natural in logic, since that is the norm for the formal languages it uses. Continuous domains come first to mind when turning to physical systems, despite the fact that systems with a discrete or quantized character often enter the fray.

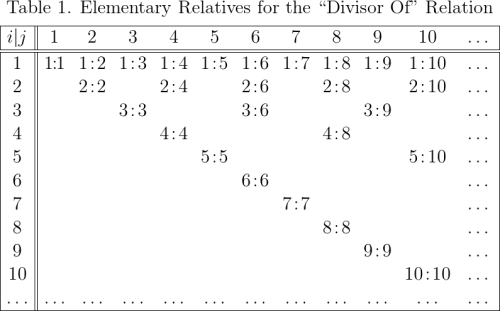
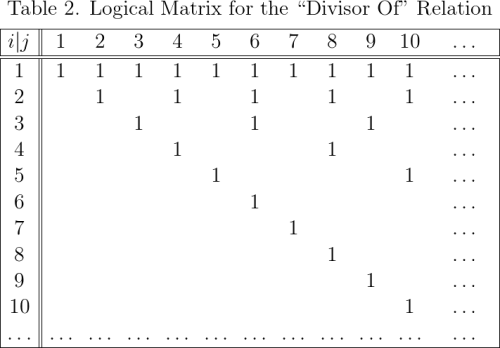
So it came as a bit of a novelty to me when my advisor, following the motto of engineers the world over to “Keep It Simple, Stupid!” — affectionately known by the acronym KISS — asked me to construct the simplest non‑trivial finite example of a sign relation I could possibly come up with. The outcome of that exercise I wrote up in the following primer on sign relations.

cc: FB | Semeiotics • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Inquiry, Logic, Logic of Relatives, Relation Theory, Semiotics, Sign Relations | Tagged C.S. Peirce, Inquiry, Logic, Logic of Relatives, Relation Theory, Semiotics, Sign Relations | 4 Comments

Peircean Semiotics and Triadic Sign Relations • 1

Posted on August 20, 2024 by Jon Awbrey

As a “guide for the perplexed”, at least when it comes to semiotics, I’ll use this thread to collect a budget of resources I think have served to clarify the topic in the past.

By way of a first offering, let me recommend the following most excellent paper, which I can say with all due modesty in light of the fact all its excellence is due to my most excellent co‑author.

Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52. Archive. Journal.
Online (doc) (pdf).

cc: FB | Semeiotics • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Logic of Relatives

Posted on August 5, 2024 by Jon Awbrey

Relations Via Relative Terms

The logic of relatives is the study of relations as represented in symbolic forms known as rhemes, rhemata, or relative terms.

Introduction

The logic of relatives, more precisely, the logic of relative terms, is the study of relations as represented in symbolic forms called rhemes, rhemata, or relative terms. The treatment of relations by way of their corresponding relative terms affords a distinctive perspective on the subject, even though all angles of approach must ultimately converge on the same formal subject matter.

The consideration of relative terms has its roots in antiquity but it entered a radically new phase of development with the work of Charles Sanders Peirce, beginning with his paper “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole’s Calculus of Logic” (1870).

References

Peirce, C.S., “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole’s Calculus of Logic”, Memoirs of the American Academy of Arts and Sciences 9, 317–378, 1870. Reprinted, Collected Papers CP 3.45–149. Reprinted, Chronological Edition CE 2, 359–429.
Online (1) (2) (3).

Readings

Aristotle, “The Categories”, Harold P. Cooke (trans.), pp. 1–109 in Aristotle, Vol. 1, Loeb Classical Library, William Heinemann, London, UK, 1938.
Aristotle, “On Interpretation”, Harold P. Cooke (trans.), pp. 111–179 in Aristotle, Vol. 1, Loeb Classical Library, William Heinemann, London, UK, 1938.
Aristotle, “Prior Analytics”, Hugh Tredennick (trans.), pp. 181–531 in Aristotle, Vol. 1, Loeb Classical Library, William Heinemann, London, UK, 1938.
Boole, George, An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities, Macmillan, 1854. Reprinted with corrections, Dover Publications, New York, NY, 1958.
Peirce, C.S., Collected Papers of Charles Sanders Peirce, Vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), Vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958. Cited as CP volume.paragraph.
Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Volume 2, 1867–1871, Peirce Edition Project (eds.), Indiana University Press, Bloomington, IN, 1984. Cited as CE 2.

Resources

cc: FB | Relation Theory • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematical Logic, Mathematics, Relation Theory, Semiotics | Tagged C.S. Peirce, Logic, Logic of Relatives, Mathematical Logic, Mathematics, Relation Theory, Semiotics | 3 Comments

Relations & Their Relatives • 4

Posted on August 3, 2024 by Jon Awbrey

From Dyadic to Triadic to Sign Relations

Peirce’s notation for elementary relatives was illustrated earlier by a dyadic relation from number theory, namely, the relation written $``{i|j}"$ for $``{i} ~\text{divides}~ {j}".$

Table 1 shows the first few ordered pairs of the relation on positive integers corresponding to the relative term, “divisor of”. Thus, the ordered pair ${i\!:\!j}$ appears in the relation if and only if ${i}$ divides ${j},$ for which the usual mathematical notation is $``{i|j}".$

Table 2 shows the same information in the form of a logical matrix. This has a coefficient of ${1}$ in row ${i}$ and column ${j}$ when ${i|j},$ otherwise it has a coefficient of ${0}.$ (The zero entries have been omitted for ease of reading.)

Just as matrices of real coefficients in linear algebra represent linear transformations, matrices of boolean coefficients represent logical transformations. The capacity of dyadic relations to generate transformations gives us part of what we need to know about the dynamics of semiosis inherent in sign relations.

The “divisor of” relation $x|y$ is a dyadic relation on the set of positive integers $\mathbb{M}$ and thus may be understood as a subset of the cartesian product $\mathbb{M} \times \mathbb{M}.$ It forms an example of a partial order relation, while the “less than or equal to” relation $x \le y$ is an example of a total order relation.

The mathematics of relations can be applied most felicitously to semiotics but there we must bump the adicity or arity up to three. We take any sign relation $L$ to be subset of a cartesian product $O \times S \times I,$ where $O$ is the set of objects under consideration in a given discussion, $S$ is the set of signs, and $I$ is the set of interpretant signs involved in the same discussion.

One thing we need to understand is the sign relation $L \subseteq O \times S \times I$ relevant to a given level of discussion may be rather more abstract than what we would call a sign process proper, that is, a structure extended through a dimension of time. Indeed, many of the most powerful sign relations generate sign processes through iteration or recursion or similar operations. In that event, the most penetrating analysis of the sign process or semiosis in view is achieved through grasping the generative sign relation at its core.

Resources

cc: FB | Relation Theory • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Category Theory, Dyadic Relations, Logic, Logic of Relatives, Logical Graphs, Mathematics, Nominalism, Peirce, Pragmatism, Realism, Relation Theory, Semiotics, Sign Relations, Triadic Relations, Visualization | Tagged C.S. Peirce, Category Theory, Dyadic Relations, Logic, Logic of Relatives, Logical Graphs, Mathematics, Nominalism, Peirce, Pragmatism, Realism, Relation Theory, Semiotics, Sign Relations, Triadic Relations, Visualization | 3 Comments

Relations & Their Relatives • 3

Posted on August 2, 2024 by Jon Awbrey

Here are two ways of looking at the divisibility relation, a dyadic relation of fundamental importance in number theory.

Just as matrices in linear algebra represent linear transformations, logical arrays and matrices represent logical transformations.

Resources

cc: FB | Relation Theory • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Relations & Their Relatives • 2

Posted on August 1, 2024 by Jon Awbrey

What is the relationship between “logical relatives” and “mathematical relations”? The word relative used as a noun in logic is short for relative term — as such it refers to an item of language used to denote a formal object.

What kind of object is that? The way things work in mathematics we are free to make up a formal object corresponding directly to the term, so long as we can form a consistent theory of it, but it’s probably easier and more practical in the long run to relate the relative term to the kinds of relations ordinarily treated in mathematics and universally applied in relational databases.

In those contexts a relation is just a set of ordered tuples and for those of us who are fans of what is called “strong typing” in computer science, such a set is always set in a specific setting, namely, it’s a subset of a specified cartesian product.

Peirce wrote $k$ -tuples $(x_1, x_2, \ldots, x_{k-1}, x_k)$ in the form $x_1 : x_2 : \ldots : x_{k-1} : x_k$ and referred to them as elementary $k$ -adic relatives. He treated a collection of $k$ -tuples as a logical aggregate or logical sum and regarded them as being arranged in $k$ -dimensional arrays.

Time for some concrete examples, which I will give in the next post.

Resources

cc: FB | Relation Theory • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Relations & Their Relatives • 1

Posted on July 31, 2024 by Jon Awbrey

Sign relations are special cases of triadic relations in much the same way binary operations in mathematics are special cases of triadic relations. It amounts to a minor complication that we participate in sign relations whenever we talk or think about anything else but it still makes sense to try and tease the separate issues apart as much as we possibly can.

As far as relations in general go, relative terms are often expressed by slotted frames like “brother of __”, “divisor of __”, and “sum of __ and __”. Peirce referred to these kinds of incomplete expressions as rhemes or rhemata and Frege used the adjective ungesättigt or unsaturated to convey more or less the same idea.

Switching the focus to sign relations, it’s fair to ask what kinds of objects might be denoted by pieces of code like “brother of __”, “divisor of __”, and “sum of __ and __”. And while we’re at it, what is this thing called denotation, anyway?

Resources

cc: FB | Relation Theory • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Relations & Their Relatives • Discussion 25

Posted on July 30, 2024 by Jon Awbrey

Re: Daniel Everett • Polyunsaturated Predicates
Re: Relations & Their Relatives • Discussion 24

Dear Daniel,

I’ve been meaning to get back to this as it keeps coming up and it’s kind of important but it took me a while to find the thread again. Just by way of jumping in and hitting the ground running I found a record of a previous discussion from the heydays and fraydays of the old Peirce List — I’ll plunder that for what it’s worth and see if I can render the main ideas any clearer this time around.

Cf: The Difference That Makes A Difference That Peirce Makes • 9
Re: Peirce List | Rheme and Reason • Jon Awbrey • Gary Fuhrman • John Sowa

The just‑so‑story that relative terms got their meanings by blanking out pieces of clauses and phrases, plus the analogies to poly‑unsaturated chemical bonds, supply a stock of engaging ways to introduce the logic of relative terms and the mathematics of relations but they both run into cul‑de‑sacs when taken too literally, and for the same reason. They tempt one to confuse the syntactic accidents used to suggest formal objects with the essential forms of the objects themselves. That is the sort of confusion that leads to syntacticism and on to its kindred nominalism.

Here’s a short note I wrote the last time questions about rhemes or rhemata came up.

I wanted to check out some impressions I formed many years ago — this would have been the late 1960s and mainly from CP 3 and 4 — about Peirce’s use of the words rhema, rheme, rhemata, etc.

Rhema, Rheme

CP 2.95, 250-265, 272, 317, 322, 379, 409n
CP 3.420-422, 465, 636
CP 4.327, 354, 395n, 403, 404, 411, 438, 439, 441, 446, 453, 461, 465, 470, 474, 504, 538n, 560, 621

Reviewing the variations and vacillations in Peirce’s usage over the years, I’ve decided to avoid the whole complex of rhematic terms for now. As I’ve come to realize more and more in recent years, analyzing and classifying signs as a substitute for analyzing and classifying objects is the first slip of a slide into nominalism, in effect, thinking the essence or reality of objects is contained in the signs we use to describe them.

Resources

Logic Syllabus

Survey of Relation Theory

cc: FB | Relation Theory • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Category Theory, Control, Cybernetics, Dyadic Relations, Information, Inquiry, Logic, Logic of Relatives, Mathematics, Relation Theory, Rheme, Semiosis, Semiotics, Sign Relations, Systems Theory, Triadic Relations | Tagged C.S. Peirce, Category Theory, Control, Cybernetics, Dyadic Relations, Information, Inquiry, Logic, Logic of Relatives, Mathematics, Relation Theory, Rheme, Semiosis, Semiotics, Sign Relations, Systems Theory, Triadic Relations | 3 Comments

Relations & Their Relatives • Discussion 24

Posted on July 28, 2024 by Jon Awbrey

Re: Daniel Everett • Polyunsaturated Predicates

DE:: Among the several ideas Peirce and Frege came up with was the idea of a predicate before and after it is linked to its arguments. Frege called the unlinked predicate unsaturated. But Peirce built this into a theory of valency. An unsaturated predicate in Frege’s system is a generic term, a rheme, in Peirce’s system. So in Peirce’s theory all languages need generic terms (rhemes) to exist. Additionally, thru his reduction thesis (a theorem proved separately by various logicians) Peirce set both the upper and lower bounds on valency which — even to this day — no other theory has done.

Dear Daniel,

In using words like “predicate” or “relation” some people mean an item of syntax, say, a verbal form with blanks substituted for a number of subject terms, and other people mean a mathematical object, say, a function $f$ from a set $X$ to a set $\mathbb{B} = \{ 0, 1 \}$ or a subset $L$ of a cartesian product $X_1 \times \ldots \times X_k.$

It would be a great service to understanding if we had a way to negotiate the gap between the above two interpretations.

To be continued …

Resources

cc: FB | Relation Theory • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Pragmatic Truth • 6

Posted on July 25, 2024 by Jon Awbrey

Peirce on Semiosis and Inquiry

Peirce’s theory of truth depends on two other, intimately related subject matters, his theory of sign relations and his theory of inquiry. Inquiry is special case of semiosis, a process passing from signs to signs while maintaining a specific relation to an object. That object may be located outside the trajectory of signs or else be found at the end of it. Inquiry includes all forms of belief revision and logical inference, including scientific method, which is what Peirce means by “the right method of transforming signs”.

A sign‑to‑sign transaction with respect to an object is a transaction involving three parties, or a relation involving three roles. A relation of that sort is called a ternary relation or a triadic relation in logic. Consequently, pragmatic theories of truth are largely expressed in terms of triadic truth predicates.

The statement above tells us one more thing: Peirce, having started out in accord with Kant, is here giving notice he is parting ways with Kant’s idea that the ultimate object of a representation is an unknowable thing‑in‑itself. Peirce would say the object is knowable, in fact, it is known in the form of its representation, however imperfectly or partially.

Reality and truth are coordinate concepts in pragmatic thinking, each being defined in relation to the other, and both together as they co‑evolve in the time evolution of inquiry. Inquiry is not a disembodied process, nor the occupation of a singular individual, but the common life of an unbounded community.

The real, then, is that which, sooner or later, information and reasoning would finally result in, and which is therefore independent of the vagaries of me and you. Thus, the very origin of the conception of reality shows that this conception essentially involves the notion of a COMMUNITY, without definite limits, and capable of an indefinite increase of knowledge. (Peirce 1868, CP 5.311).

Different minds may set out with the most antagonistic views, but the progress of investigation carries them by a force outside of themselves to one and the same conclusion. This activity of thought by which we are carried, not where we wish, but to a foreordained goal, is like the operation of destiny. No modification of the point of view taken, no selection of other facts for study, no natural bent of mind even, can enable a man to escape the predestinate opinion. This great law is embodied in the conception of truth and reality. The opinion which is fated to be ultimately agreed to by all who investigate, is what we mean by the truth, and the object represented in this opinion is the real. That is the way I would explain reality. (Peirce 1878, CP 5.407).

Resources

cc: FB | Inquiry Driven Systems • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Aristotle, C.S. Peirce, Coherence, Concordance, Congruence, Consensus, Convergence, Correspondence, Dewey, Fixation of Belief, Information, Inquiry, John Dewey, Kant, Logic, Logic of Science, Method, Peirce, Philosophy, Pragmatic Maxim, Pragmatism, Semiotics, Sign Relations, Triadic Relations, Truth, Truth Theory, William James | Tagged Aristotle, C.S. Peirce, Coherence, Concordance, Congruence, Consensus, Convergence, Correspondence, Dewey, Fixation of Belief, Information, Inquiry, John Dewey, Kant, Logic, Logic of Science, Method, Peirce, Philosophy, Pragmatic Maxim, Pragmatism, Semiotics, Sign Relations, Triadic Relations, Truth, Truth Theory, William James | 4 Comments

	Survey of Differenti… on Differential Logic • 3
	Survey of Differenti… on Differential Logic • 2
	Survey of Differenti… on Differential Logic • 1
	Survey of Differenti… on Differential Logic • Over…
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 3
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…

Share this:

Share this:

Introduction

References

Readings

Resources

Share this:

From Dyadic to Triadic to Sign Relations

Resources

Share this:

Resources

Share this:

Resources

Share this:

Resources

Share this:

Rhema, Rheme

Resources

Share this:

Resources

Share this:

Peirce on Semiosis and Inquiry

Resources

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta