Peirce on Reality, Signs, Truth
Very little in Peirce’s thought can be understood in its proper light without understanding he thinks all thoughts are signs, and thus, according to his theory of thought, no thought is understandable outside the context of a sign relation. Sign relations taken collectively are the subject matter of a theory of signs. So Peirce’s semeiotic, his theory of sign relations, is key to understanding his entire philosophy of pragmatic thinking.
In his contribution to the article “Truth and Falsity and Error” for Baldwin’s Dictionary of Philosophy and Psychology (1901), Peirce defines truth in the following way.
Truth is that concordance of an abstract statement with the ideal limit towards which endless investigation would tend to bring scientific belief, which concordance the abstract statement may possess by virtue of the confession of its inaccuracy and one‑sidedness, and this confession is an essential ingredient of truth. (Peirce 1901, CP 5.565).
This statement emphasizes Peirce’s view that ideas of approximation, incompleteness, and partiality, what he describes elsewhere as fallibilism and “reference to the future”, are essential to a proper conception of truth. Though Peirce occasionally uses words like concordance and correspondence to describe one aspect of the pragmatic sign relation, he is also quite explicit in saying that definitions of truth based on mere correspondence are no more than nominal definitions, which he follows long tradition in relegating to a lower status than real definitions.
That truth is the correspondence of a representation with its object is, as Kant says, merely the nominal definition of it. Truth belongs exclusively to propositions. A proposition has a subject (or set of subjects) and a predicate. The subject is a sign; the predicate is a sign; and the proposition is a sign that the predicate is a sign of that of which the subject is a sign. If it be so, it is true. But what does this correspondence or reference of the sign, to its object, consist in? (Peirce 1906, CP 5.553).
Peirce makes a statement here which is critical to understanding the relationship between his pragmatic definition of truth and any theory of truth which leaves it solely and simply a matter of representations corresponding with their objects. Peirce, like Kant before him, recognizes Aristotle’s distinction between a nominal definition, a definition in name only, and a real definition, one which states the function of the concept, the vera causa or reason for conceiving it, and so indicates the essence, the underlying substance of its object. This tells us the sense in which Peirce entertained a correspondence theory of truth, namely, a purely nominal sense. To get beneath the superficiality of the nominal definition it is necessary to analyze the notion of correspondence in greater depth.
In preparing for this task, Peirce makes use of an allegorical story, omitted here, the moral of which tells us there is no use seeking a conception of truth which we cannot conceive ourselves being able to capture in a humanly conceivable concept. So we might as well proceed on the assumption that we have a real hope of comprehending the answer, of being able to “handle the truth” when the time comes. Bearing that in mind, the problem of defining truth reduces to the following form.
Now thought is of the nature of a sign. In that case, then, if we can find out the right method of thinking and can follow it out — the right method of transforming signs — then truth can be nothing more nor less than the last result to which the following out of this method would ultimately carry us. In that case, that to which the representation should conform, is itself something in the nature of a representation, or sign — something noumenal, intelligible, conceivable, and utterly unlike a thing‑in‑itself. (Peirce 1906, CP 5.553).
Resources
cc: FB | Inquiry Driven Systems • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
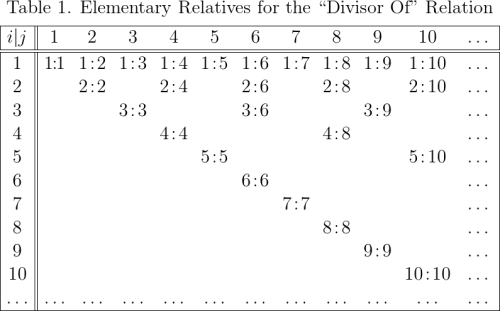
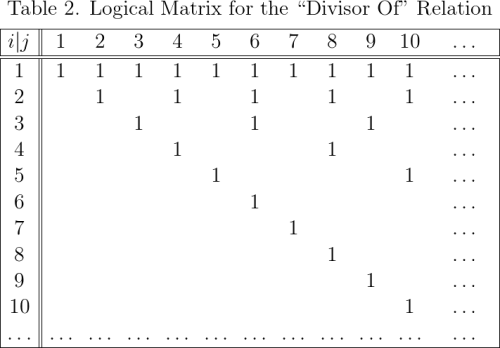
appears in the relation if and only if
divides
for which the usual mathematical notation is
in row
and column
when
otherwise it has a coefficient of
(The zero entries have been omitted for ease of reading.)