Inquiry Into Inquiry

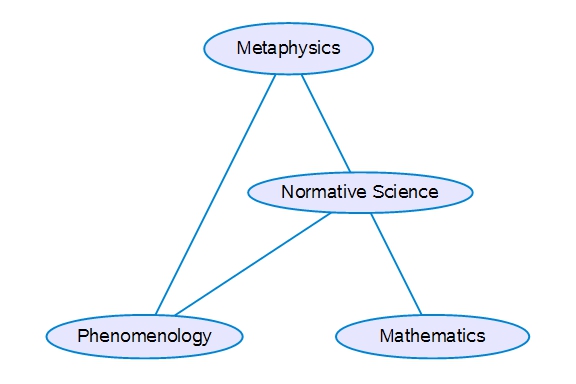
Peirce clearly set great store by his 1902 definition of logic as formal semiotic, whose principles he proposed to deduce by evident and rigorous mathematical reasoning from his triadic relational definition of a sign.

It is from this definition, together with a definition of “formal”, that I deduce mathematically the principles of logic.  (NEM 4, 21).

It is from this definition that I deduce the principles of logic by mathematical reasoning, and by mathematical reasoning that, I aver, will support criticism of Weierstrassian severity, and that is perfectly evident.  (NEM 4, 54).

By “criticism of Weierstrassian severity”, Peirce refers to the reconstitution of mathematical analysis precipitated by Karl Weierstrass during the latter part of the 19th Century, replacing many intuitive but problematic concepts with exacting enough definitions to support the development of coherent and powerful theories.

That bit of history teaches an important lesson. Not every form of words that might be cast about an intuitive object or used to express an intuitive concept will exhibit the strength of a formal definition, one that supports mathematical reasoning from evident truths and allows the deduction of a coherent and comprehensive theory of its object domain, for example, in our present instance, “the principles of logic”.

The moral of the story so far is to recognize the qualifications of these “industrial strength” definitions, and to realize what it means for Peirce to be advertizing these very virtues for his 1902 brand of sign definition.

cc: Inquiry List • Peirce List (1) (2) (3)

Re: Peirce List • Gary Fuhrman (1) (2)

The following two passages may help to clarify Peirce’s admittedly peculiar usage of “formal” in this context.

• C.S. Peirce • Objective Logic
• C.S. Peirce • Logic as Semiotic

Re: Peirce List • Jim Willgoose (1) (2)

We discussed that passage on Objective Logic a little while back, until we reached the customary fork of diverging interpretations.  The relation between classical logic and its supposed alternatives is a current interest of mine but I can see no alternative except to view it from the classical side.  This may be accountable to the way modalities, from impossible to possible and contingent to necessary, are viewed by the Platonic realist mathematician.  What is possible is real and thus realized in the requisite space of possibility.  So the possible may be surveyed, at any rate at the end of inquiry, in accord with the way its real extension rests arrayed under its comprehension.  Of course you see the catch — “at the end of inquiry” — and there the rub must be left to its itch, for now.

But I cited that passage this time around only for the sake of collating its introduction, “Logic, in the sense of Normative Semeotic”, with the words of Peirce’s definition, “Logic will here be defined as formal semiotic”, giving us reason to say Peirce equates formal with normative in this frame.

cc: Inquiry List • Peirce List (1) (2) (3)

Walking the line between phenomenology and mathematics, let us cast our eyes on the prize of defining logic.  Peirce defines logic as formal semiotic — and that in turn calls for a definition of sign.

Here is a place where he defines logic and signs in one deft pass —

• C.S. Peirce • On the Definition of Logic

Peirce defines logic as formal semiotic.  We know semiotic is the doctrine or theory of signs, but the current passage leaves us with a promissory note on the meaning of formal.  Luckily, though, it is easy enough to find other places where he tells us that formal is pragmatically synonymous with normative, and that puts logic squarely within the normative sciences, as classical tradition always said it ought to be.

Peirce defines a sign in relational terms, as one role out of three, the other two roles being the role of its interpretant sign and the role of its object.  This is a very different matter from defining an essence, that is, an inalienable, inherent, intrinsic property of a “thing in itself”.

Peirce is emphatic about the independence of his joint definition from any reference to human cognition, just as normative sciences ought to be orthogonal to descriptive sciences, and yet he insists that his “non-psychological conception of logic” virtually inheres in the general idea of logic, however incognito it may abide there.

cc: Inquiry List • Peirce List (1) (2) (3)

If I hear what a couple of my interlocutors are saying, we need both a place to stand and direction of focus in order to tackle the massa confusa that rises up like a great cloud of unknowing every time we inquire into any topic of significance that is covered by Peirce’s writings.

I think I can see the wisdom in that …

For a place to stand, let’s adopt Peirce’s own two-footed and thrice-braced standing, a stance I like to picture in the following manner:

Normative science rests largely on phenomenology and on mathematics;
metaphysics on phenomenology and on normative science.

❧ Charles Sanders Peirce • Collected Papers, CP 1.186 (1903)
Syllabus • Classification of Sciences (CP 1.180–202, G-1903-2b)

Peirce’s formula says a large number of very important things about the relationship among logic (a normative science), mathematics, metaphysics, and phenomenology.  For one thing, he recognizes the classical distinction between descriptive sciences and normative sciences, which have independent objectives even when they survey the same domains of data.  For another, he allows for the collaborative or complementary duties of phenomenology, the observation of what appears in experience, and mathematics, the exploration of possible forms of existence.  In scientific types of inquiry, phenomenology and mathematics operate in tandem, the one supplying a stream of observational data and the other fitting its evolving stock of models and theories to the flux in hopes of finding or making one that makes partial sense of it all.

That will serve as a place and a stance to start.
Next to mark a few points of direction and focus.

cc: Inquiry List • Peirce List (1) (2) (3)

Re: Peirce List • Rafe Champion (1) (2)

Where to begin?  Perhaps in the middle …

In the early 90s — having spent a quarter of a century acquiring a bachelor’s in “Mathematical and Philosophical Method”, a master’s in mathematics, and master’s in psychology — I returned to grad school in a Systems Engineering program with the aim of “unifying the manifold” of unfinished projects I had begun in the years gone by.

My study of Peirce went back to my freshman year in college and many of my unfinished projects involved the development and extension of his ideas in one way or another.  The application to grad school asked for a statement of my current research interests.  I wrote out an eighty page essay, of which I submitted 20 pages plus a 20 page bibliography, being what I considered the more settled part of the overall vision.

There’s a copy of that here:

• Prospects for Inquiry Driven Systems

That may provide an indication of what I still regard as worthy goals but of course few people will ever read much of that, so I’ll make the old college try to succintify it as we go.

cc: Inquiry List • Peirce List (1) (2) (3)

Recent discussions have brought to mind a number of persistent problems in pragmatic thought, especially if we aim to apply Peirce’s conceptions to real practical effect in understanding pressing real-world phenomena.  Among the host of issues, the following two objectives rise to the fore.

1. To clarify the concept of a sign relation to the point where a full-fledged theory of signs can be developed on the basis of the resulting definition.
2. To comprehend semiosis, that is, the variety of sign processes, in a fully dynamic fashion, by augmenting the bare definition of a sign relation with a temporal dimension and the capacity to formulate laws of possibly goal-oriented temporal evolution.

Anyway, that’s the plan.

But I have a bunch of wikifying or maybe blogging to do before I can get back to work on the substantial issues.

cc: Inquiry List • Peirce List (1) (2) (3)

It looks like we might be due for one of our recurring reviews on the closely related subjects of definition and determination, with special reference to what Peirce himself wrote on the topics.

Arisbe List Archive

Here is a collection of excerpts on the subject of determination, mostly from Peirce but with a sampling of thoughts from other thinkers before and after him, on account of the larger questions of determinacy I was pursuing at the time

• Excerpts on Determination • May 2001 • Aug 2001

Collection Of Source Materials

One naturally looks to the Baldwin and Century dictionaries for Peirce-connected definitions of definition but I’d like to start with a series of texts I think are closer to Peirce’s own thoughts on definition, where he is not duty-bound to give a compendious account of every significant thinker’s point of view.  It may be a while before I get all the excerpts copied out.

• Excerpts on Definition
• Excerpts on Determination

cc: Inquiry List • Peirce List (1) (2) (3)