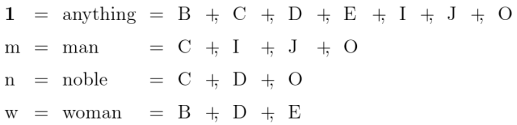Peirce’s 1870 “Logic of Relatives” • Comment 9.4

Posted on February 27, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 9.4

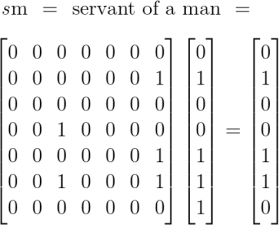
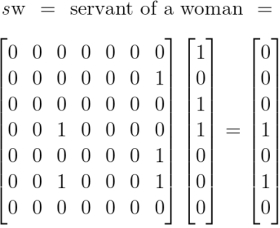
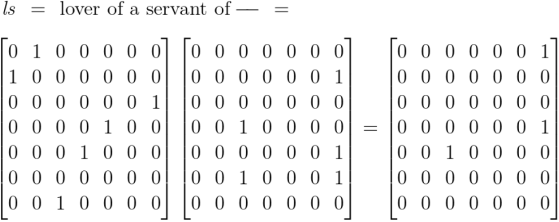
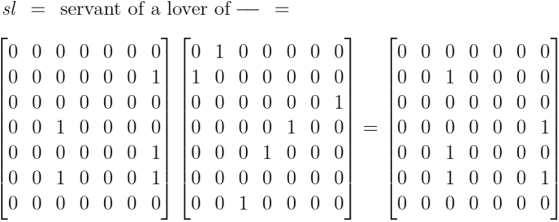
Boole rationalizes the properties of what we now call boolean multiplication, roughly equivalent to logical conjunction, by means of his concept of selective operations.  Peirce, in his turn, taking a radical step of analysis which has seldom been recognized for what it would lead to, does not consider this multiplication a fundamental operation, but derives it as a by-product of relative multiplication by a comma relative.  In this way Peirce makes logical conjunction a special case of relative composition.

This opens up a wide field of inquiry, the operational significance of logical terms, but it will be best to advance bit by bit and to lean on simple examples.

Back to Venice and the close-knit party of absolutes and relatives we entertained when last stopping there.

Here is the list of absolute terms we had been considering before:

Absolute Terms 1 M N W

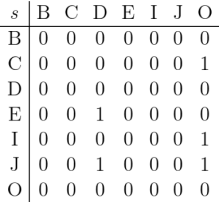
Here is the list of comma inflexions or diagonal extensions of those terms:

\begin{array}{lll} \mathbf{1,} & = & \text{anything that is}\, \underline{~~~~} \\[6pt] & = & \mathrm{B\!:\!B} ~+\!\!,~ \mathrm{C\!:\!C} ~+\!\!,~ \mathrm{D\!:\!D} ~+\!\!,~ \mathrm{E\!:\!E} ~+\!\!,~ \mathrm{I\!:\!I} ~+\!\!,~ \mathrm{J\!:\!J} ~+\!\!,~ \mathrm{O\!:\!O} \\[9pt] \mathrm{m,} & = & \text{man that is}\, \underline{~~~~} \\[6pt] & = & \mathrm{C\!:\!C} ~+\!\!,~ \mathrm{I\!:\!I} ~+\!\!,~ \mathrm{J\!:\!J} ~+\!\!,~ \mathrm{O\!:\!O} \\[9pt] \mathrm{n,} & = & \text{noble that is}\, \underline{~~~~} \\[6pt] & = & \mathrm{C\!:\!C} ~+\!\!,~ \mathrm{D\!:\!D} ~+\!\!,~ \mathrm{O\!:\!O} \\[9pt] \mathrm{w,} & = & \text{woman that is}\, \underline{~~~~} \\[6pt] & = & \mathrm{B\!:\!B} ~+\!\!,~ \mathrm{D\!:\!D} ~+\!\!,~ \mathrm{E\!:\!E} \end{array}

One observes the diagonal extension of \mathbf{1} is the same thing as the identity relation \mathit{1}.

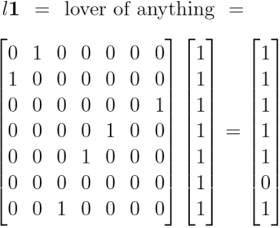
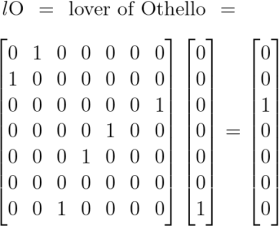
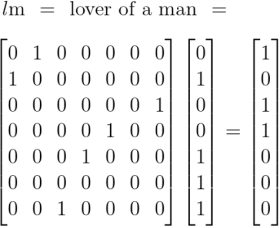
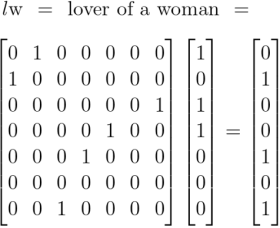
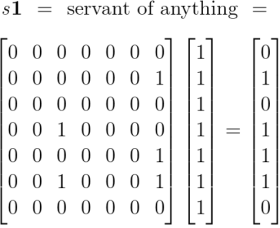
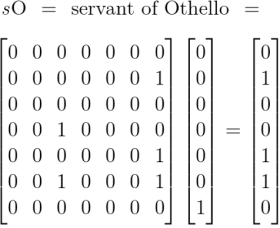
Earlier we computed the following products, obtained by applying the diagonal extensions of absolute terms to the same set of absolute terms.

\begin{array}{lllll} \mathrm{m},\!\mathrm{n} & = & \text{man that is a noble} & = & \mathrm{C} ~+\!\!,~ \mathrm{O} \\[6pt] \mathrm{n},\!\mathrm{m} & = & \text{noble that is a man} & = & \mathrm{C} ~+\!\!,~ \mathrm{O} \\[6pt] \mathrm{w},\!\mathrm{n} & = & \text{woman that is a noble} & = & \mathrm{D} \\[6pt] \mathrm{n},\!\mathrm{w} & = & \text{noble that is a woman} & = & \mathrm{D} \end{array}

From that we take our first clue why the commutative law holds for logical conjunction.  More in the way of practical insight could be had by working systematically through the collection of products generated by the operational means at hand, namely, the products obtained by appending a comma to each of the terms \mathbf{1}, \mathrm{m}, \mathrm{n}, \mathrm{w} then applying the resulting relatives to those selfsame terms again.

Before we venture into that territory, however, let us equip our intuitions with the forms of graphical and matrical representation which served us so well in our previous adventures.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in Boole, Boolean Algebra, C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Visualization | Tagged , , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 9.3

Posted on February 26, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 9.3

An idempotent element x in an algebraic system is one which obeys the idempotent law, that is, it satisfies the equation xx = x.  Under most circumstances it is usual to write this as x^2 = x.

If the algebraic system in question falls under the additional laws necessary to carry out the required transformations then x^2 = x is convertible to x - x^2 = 0, and this in turn to x(1 - x) = 0.

If the algebraic system satisfies the requirements of a boolean algebra then the equation x(1 - x) = 0 amounts to saying x \land \lnot x is identically false, in effect, a statement of the classical principle of non‑contradiction.

We have already seen how Boole found rationales for the commutative law and the idempotent law by contemplating the properties of selective operations.

It is time to bring these threads together, which we can do by considering the so-called idempotent representation of sets.  This will give us one of the best ways to understand the significance Boole attaches to selective operations.  It will also link up with the statements Peirce makes regarding his dimension-raising comma operation.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in Boole, Boolean Algebra, C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Visualization | Tagged , , , , , , , | 11 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 9.2

Posted on February 26, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 9.2

In setting up his discussion of selective operations and their corresponding selective symbols, Boole writes the following.

The operation which we really perform is one of selection according to a prescribed principle or idea.  To what faculties of the mind such an operation would be referred, according to the received classification of its powers, it is not important to inquire, but I suppose that it would be considered as dependent upon the two faculties of Conception or Imagination, and Attention.  To the one of these faculties might be referred the formation of the general conception;  to the other the fixing of the mental regard upon those individuals within the prescribed universe of discourse which answer to the conception.  If, however, as seems not improbable, the power of Attention is nothing more than the power of continuing the exercise of any other faculty of the mind, we might properly regard the whole of the mental process above described as referrible to the mental faculty of Imagination or Conception, the first step of the process being the conception of the Universe itself, and each succeeding step limiting in a definite manner the conception thus formed.  Adopting this view, I shall describe each such step, or any definite combination of such steps, as a definite act of conception.

(Boole, Laws of Thought, 43)

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in Boole, Boolean Algebra, C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Visualization | Tagged , , , , , , , | 11 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 9.1

Posted on February 24, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 9.1

Perspective on Peirce’s use of the comma operator at CP 3.73 and CP 3.74 can be gained by dropping back a few years and seeing how George Boole explained his twin conceptions of selective operations and selective symbols.

Let us then suppose that the universe of our discourse is the actual universe, so that words are to be used in the full extent of their meaning, and let us consider the two mental operations implied by the words “white” and “men”.  The word “men” implies the operation of selecting in thought from its subject, the universe, all men;  and the resulting conception, men, becomes the subject of the next operation.  The operation implied by the word “white” is that of selecting from its subject, “men”, all of that class which are white.  The final resulting conception is that of “white men”.

Now it is perfectly apparent that if the operations above described had been performed in a converse order, the result would have been the same.  Whether we begin by forming the conception of “men”, and then by a second intellectual act limit that conception to “white men”, or whether we begin by forming the conception of “white objects”, and then limit it to such of that class as are “men”, is perfectly indifferent so far as the result is concerned.  It is obvious that the order of the mental processes would be equally indifferent if for the words “white” and “men” we substituted any other descriptive or appellative terms whatever, provided only that their meaning was fixed and absolute.  And thus the indifference of the order of two successive acts of the faculty of Conception, the one of which furnishes the subject upon which the other is supposed to operate, is a general condition of the exercise of that faculty.  It is a law of the mind, and it is the real origin of that law of the literal symbols of Logic which constitutes its formal expression, [xy = yx]. 

It is equally clear that the mental operation above described is of such a nature that its effect is not altered by repetition.  Suppose that by a definite act of conception the attention has been fixed upon men, and that by another exercise of the same faculty we limit it to those of the race who are white.  Then any further repetition of the latter mental act, by which the attention is limited to white objects, does not in any way modify the conception arrived at, viz., that of white men.  This is also an example of a general law of the mind, and it has its formal expression in the law [x^2 = x] of the literal symbols.

(Boole, Laws of Thought, 44–45)

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in Boole, Boolean Algebra, C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Visualization | Tagged , , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 9

Posted on February 23, 2014 by Jon Awbrey

We continue with §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 9

The Signs for Multiplication (cont.)

It is obvious that multiplication into a multiplicand indicated by a comma is commutative,1 that is,

\mathit{s},\!\mathit{l} ~=~ \mathit{l},\!\mathit{s}

This multiplication is effectively the same as that of Boole in his logical calculus.  Boole’s unity is my \mathbf{1}, that is, it denotes whatever is.

  1. It will often be convenient to speak of the whole operation of affixing a comma and then multiplying as a commutative multiplication, the sign for which is the comma.  But though this is allowable, we shall fall into confusion at once if we ever forget that in point of fact it is not a different multiplication, only it is multiplication by a relative whose meaning — or rather whose syntax — has been slightly altered;  and that the comma is really the sign of this modification of the foregoing term.

(Peirce, CP 3.74)

References

  • Peirce, C.S. (1870), “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole’s Calculus of Logic”, Memoirs of the American Academy of Arts and Sciences 9, 317–378, 26 January 1870.  Reprinted, Collected Papers 3.45–149, Chronological Edition 2, 359–429.  Online (1) (2) (3).
  • Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958.
  • Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 11 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 8.6

Posted on February 23, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 8.6

The foregoing has hopefully filled in enough background that we can begin to make sense of the more mysterious parts of CP 3.73.

The Signs for Multiplication (cont.)

Thus far, we have considered the multiplication of relative terms only.  Since our conception of multiplication is the application of a relation, we can only multiply absolute terms by considering them as relatives.

Now the absolute term “man” is really exactly equivalent to the relative term “man that is ──”, and so with any other.  I shall write a comma after any absolute term to show that it is so regarded as a relative term.

Then “man that is black” will be written:

\mathrm{m},\!\mathrm{b}.

(CP 3.73)

In any system where elements are organized according to types there tend to be any number of ways in which elements of one type are naturally associated with elements of another type.  If the association is anything like a logical equivalence, but with the first type being lower and the second type being higher in some sense, then one may speak of a semantic ascent from the lower to the higher type.

For example, it is common in mathematics to associate an element a of a set A with the constant function f_a : X \to A which has f_a (x) = a for all x in X, where X is an arbitrary set which is fixed in the context of discussion.  Indeed, the correspondence is so close that one often uses the same name {}^{\backprime\backprime} a {}^{\prime\prime} to denote both the element a in A and the function a = f_a : X \to A, relying on context or an explicit type indication to tell them apart.

For another example, we have the tacit extension of a k-place relation L \subseteq X_1 \times \ldots \times X_k to a (k+1)-place relation L' \subseteq X_1 \times \ldots \times X_{k+1} which we get by letting L' = L \times X_{k+1}, that is, by maintaining the constraints of L on the first k variables and letting the last variable wander freely.

What we have here, if I understand Peirce correctly, is another such type of natural extension, sometimes called the diagonal extension.  This extension associates a k-adic relative or a k-adic relation, counting the absolute term and the set whose elements it denotes as the cases for k = 0, with a series of relatives and relations of higher adicities.

A few examples will suffice to anchor these ideas.

Absolute Terms

\begin{array}{*{11}{c}} \mathrm{m} & = & \text{man} & = & \mathrm{C} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \\[6pt] \mathrm{n} & = & \text{noble} & = & \mathrm{C} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{O} \\[6pt] \mathrm{w} & = & \text{woman} & = & \mathrm{B} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} \end{array}

Diagonal Extensions

\begin{array}{*{11}{c}} \mathrm{m,} & = & \text{man that is}\, \underline{~~~~} & = & \mathrm{C\!:\!C} & +\!\!, & \mathrm{I\!:\!I} & +\!\!, & \mathrm{J\!:\!J} & +\!\!, & \mathrm{O\!:\!O} \\[6pt] \mathrm{n,} & = & \text{noble that is}\, \underline{~~~~} & = & \mathrm{C\!:\!C} & +\!\!, & \mathrm{D\!:\!D} & +\!\!, & \mathrm{O\!:\!O} \\[6pt] \mathrm{w,} & = & \text{woman that is}\, \underline{~~~~} & = & \mathrm{B\!:\!B} & +\!\!, & \mathrm{D\!:\!D} & +\!\!, & \mathrm{E\!:\!E} \end{array}

Sample Products

\begin{array}{lll} \mathrm{m},\!\mathrm{n} & = & \text{man that is a noble} \\[6pt] & = & (\mathrm{C\!:\!C} ~+\!\!,~ \mathrm{I\!:\!I} ~+\!\!,~ \mathrm{J\!:\!J} ~+\!\!,~ \mathrm{O\!:\!O}) \\ & & \times \\ & & (\mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{O}) \\[6pt] & = & \mathrm{C} ~+\!\!,~ \mathrm{O} \end{array}

\begin{array}{lll} \mathrm{n},\!\mathrm{m} & = & \text{noble that is a man} \\[6pt] & = & (\mathrm{C\!:\!C} ~+\!\!,~ \mathrm{D\!:\!D} ~+\!\!,~ \mathrm{O\!:\!O}) \\ & & \times \\ & & (\mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) \\[6pt] & = & \mathrm{C} ~+\!\!,~ \mathrm{O} \end{array}

\begin{array}{lll} \mathrm{w},\!\mathrm{n} & = & \text{woman that is a noble} \\[6pt] & = & (\mathrm{B\!:\!B} ~+\!\!,~ \mathrm{D\!:\!D} ~+\!\!,~ \mathrm{E\!:\!E}) \\ & & \times \\ & & (\mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{O}) \\[6pt] & = & \mathrm{D} \end{array}

\begin{array}{lll} \mathrm{n},\!\mathrm{w} & = & \text{noble that is a woman} \\[6pt] & = & (\mathrm{C\!:\!C} ~+\!\!,~ \mathrm{D\!:\!D} ~+\!\!,~ \mathrm{O\!:\!O}) \\ & & \times \\ & & (\mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E}) \\[6pt] & = & \mathrm{D} \end{array}

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Matrices, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 8.5

Posted on February 20, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 8.5

I continue with my commentary on CP 3.73, developing the Othello example as a way of illustrating Peirce’s formalism.

Since multiplication by a dyadic relative term is a logical analogue of matrix multiplication in linear algebra, all the products computed above can be represented by logical matrices, that is, by arrays of boolean \{ 0, 1 \} coordinate values.  Absolute terms and dyadic relatives are represented as 1-dimensional and 2-dimensional arrays, respectively.

The equations defining the absolute terms are given again below, first as logical sums of individual terms and then as n-tuples of boolean coordinates.

Othello Universe

Since we are going to be regarding these tuples as column arrays, it is convenient to arrange them in a table of the following form.

Othello Column Array

Here are the dyadic relative terms again, followed by their representation as coefficient matrices, in this case bordered by row and column labels to remind us what the coefficient values are meant to signify.

\begin{array}{*{13}{c}} \mathit{l} & = & \mathrm{B\!:\!C} & +\!\!, & \mathrm{C\!:\!B} & +\!\!, & \mathrm{D\!:\!O} & +\!\!, & \mathrm{E\!:\!I} & +\!\!, & \mathrm{I\!:\!E} & +\!\!, & \mathrm{O\!:\!D} \end{array}

Logical Matrix L

\begin{array}{*{13}{c}} \mathit{s} & = & \mathrm{C\!:\!O} & +\!\!, & \mathrm{E\!:\!D} & +\!\!, & \mathrm{I\!:\!O} & +\!\!, & \mathrm{J\!:\!D} & +\!\!, & \mathrm{J\!:\!O} \end{array}

Logical Matrix S

Here are the matrix representations of the products we calculated before.

Logical Matrix L1

Logical Matrix LO

Logical Matrix LM

Logical Matrix LW

Logical Matrix S1

Logical Matrix SO

Logical Matrix SM

Logical Matrix SW

Logical Matrix LS

Logical Matrix SL

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Matrices, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 8.4

Posted on February 19, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 8.4

I continue with my commentary on CP 3.73, developing the Othello example as a way of illustrating Peirce’s formalism.

To familiarize ourselves with the forms of calculation available in Peirce’s notation, let us compute a few of the simplest products we find at hand in the Othello universe.

Here are the absolute terms:

\begin{array}{*{15}{c}} \mathbf{1} & = & \mathrm{B} & +\!\!, & \mathrm{C} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \\[6pt] \mathrm{b} & = & \mathrm{O} \\[6pt] \mathrm{m} & = & \mathrm{C} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \\[6pt] \mathrm{w} & = & \mathrm{B} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} \end{array}

Here are the dyadic relative terms:

\begin{array}{*{13}{c}} \mathit{l} & = & \mathrm{B} \!:\! \mathrm{C} & +\!\!, & \mathrm{C} \!:\! \mathrm{B} & +\!\!, & \mathrm{D} \!:\! \mathrm{O} & +\!\!, & \mathrm{E} \!:\! \mathrm{I} & +\!\!, & \mathrm{I} \!:\! \mathrm{E} & +\!\!, & \mathrm{O} \!:\! \mathrm{D} \\[6pt] \mathit{s} & = & \mathrm{C} \!:\! \mathrm{O} & +\!\!, & \mathrm{E} \!:\! \mathrm{D} & +\!\!, & \mathrm{I} \!:\! \mathrm{O} & +\!\!, & \mathrm{J} \!:\! \mathrm{D} & +\!\!, & \mathrm{J} \!:\! \mathrm{O} \end{array}

Here are a few of the simplest products among those terms:

\begin{array}{lll} \mathit{l}\mathbf{1} & = & \text{lover of anything} \\[6pt] & = & (\mathrm{B} \!:\! \mathrm{C} ~+\!\!,~ \mathrm{C} \!:\! \mathrm{B} ~+\!\!,~ \mathrm{D} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{I} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{E} ~+\!\!,~ \mathrm{O} \!:\! \mathrm{D}) \\ & & \times \\ & & (\mathrm{B} ~+\!\!,~ \mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) \\[6pt] & = & \mathrm{B} ~+\!\!,~ \mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{O} \\[6pt] & = & \text{anything except} ~ \mathrm{J} \end{array}

\begin{array}{lll} \mathit{l}\mathrm{O} & = & \text{lover of Othello} \\[6pt] & = & (\mathrm{B} \!:\! \mathrm{C} ~+\!\!,~ \mathrm{C} \!:\! \mathrm{B} ~+\!\!,~ \mathrm{D} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{I} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{E} ~+\!\!,~ \mathrm{O} \!:\! \mathrm{D}) \\ & & \times \\ & & \mathrm{O} \\[6pt] & = & \mathrm{D} \end{array}

\begin{array}{lll} \mathit{l}\mathrm{m} & = & \text{lover of a man} \\[6pt] & = & (\mathrm{B} \!:\! \mathrm{C} ~+\!\!,~ \mathrm{C} \!:\! \mathrm{B} ~+\!\!,~ \mathrm{D} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{I} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{E} ~+\!\!,~ \mathrm{O} \!:\! \mathrm{D}) \\ & & \times \\ & & (\mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) \\[6pt] & = & \mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E} \end{array}

\begin{array}{lll} \mathit{l}\mathrm{w} & = & \text{lover of a woman} \\[6pt] & = & (\mathrm{B} \!:\! \mathrm{C} ~+\!\!,~ \mathrm{C} \!:\! \mathrm{B} ~+\!\!,~ \mathrm{D} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{I} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{E} ~+\!\!,~ \mathrm{O} \!:\! \mathrm{D}) \\ & & \times \\ & & (\mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E}) \\[6pt] & = & \mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{O} \end{array}

\begin{array}{lll} \mathit{s}\mathbf{1} & = & \text{servant of anything} \\[6pt] & = & (\mathrm{C} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{O}) \\ & & \times \\ & & (\mathrm{B} ~+\!\!,~ \mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) \\[6pt] & = & \mathrm{C} ~+\!\!,~ \mathrm{E} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} \end{array}

\begin{array}{lll} \mathit{s}\mathrm{O} & = & \text{servant of Othello} \\[6pt] & = & (\mathrm{C} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{O}) \\ & & \times \\ & & \mathrm{O} \\[6pt] & = & \mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} \end{array}

\begin{array}{lll} \mathit{s}\mathrm{m} & = & \text{servant of a man} \\[6pt] & = & (\mathrm{C} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{O}) \\ & & \times \\ & & (\mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) \\[6pt] & = & \mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} \end{array}

\begin{array}{lll} \mathit{s}\mathrm{w} & = & \text{servant of a woman} \\[6pt] & = & (\mathrm{C} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{O}) \\ & & \times \\ & & (\mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E}) \\[6pt] & = & \mathrm{E} ~+\!\!,~ \mathrm{J} \end{array}

\begin{array}{lll} \mathit{l}\mathit{s} & = & \text{lover of a servant of}\, \underline{~~~~} \\[6pt] & = & (\mathrm{B} \!:\! \mathrm{C} ~+\!\!,~ \mathrm{C} \!:\! \mathrm{B} ~+\!\!,~ \mathrm{D} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{I} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{E} ~+\!\!,~ \mathrm{O} \!:\! \mathrm{D}) \\ & & \times \\ & & (\mathrm{C} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{O}) \\[6pt] & = & \mathrm{B} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{D} \end{array}

\begin{array}{lll} \mathit{s}\mathit{l} & = & \text{servant of a lover of}\, \underline{~~~~} \\[6pt] & = & (\mathrm{C} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{O}) \\ & & \times \\ & & (\mathrm{B} \!:\! \mathrm{C} ~+\!\!,~ \mathrm{C} \!:\! \mathrm{B} ~+\!\!,~ \mathrm{D} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{I} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{E} ~+\!\!,~ \mathrm{O} \!:\! \mathrm{D}) \\[6pt] & = & \mathrm{C} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{E} \!:\! \mathrm{O} ~+\!\!,~ \mathrm{I} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{D} ~+\!\!,~ \mathrm{J} \!:\! \mathrm{O} \end{array}

Among other things, one observes that the relative terms \mathit{l} and \mathit{s} do not commute, that is, \mathit{l}\mathit{s} is not equal to \mathit{s}\mathit{l}.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 8.3

Posted on February 18, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 8.3

I continue with my commentary on CP 3.73, developing the Othello example as a way of illustrating Peirce’s formalism.

It is critically important to distinguish a relation from a relative term.

  • The relation is an object of thought which may be regarded in extension as a set of ordered tuples known as its elementary relations.
  • The relative term is a sign which denotes certain objects, called its relates, as these are determined in relation to certain other objects, called its correlates.  Under most circumstances the relative term may be taken to denote the corresponding relation.

Returning to the Othello example, let us consider the dyadic relatives ^{\backprime\backprime} \text{lover of}\, \underline{~~~~}\, ^{\prime\prime} and ^{\backprime\backprime} \text{servant of}\, \underline{~~~~}\, ^{\prime\prime}.

The relative term \mathit{l} equivalent to the rhematic expression ^{\backprime\backprime} \text{lover of}\, \underline{~~~~}\, ^{\prime\prime} is given by the following equation.

\begin{array}{*{13}{c}} \mathit{l} & = & \mathrm{B} \!:\! \mathrm{C} & +\!\!, & \mathrm{C} \!:\! \mathrm{B} & +\!\!, & \mathrm{D} \!:\! \mathrm{O} & +\!\!, & \mathrm{E} \!:\! \mathrm{I} & +\!\!, & \mathrm{I} \!:\! \mathrm{E} & +\!\!, & \mathrm{O} \!:\! \mathrm{D} \end{array}

In the interests of simplicity, let’s put aside all distinctions of rank and fealty, collapsing the motley crews of servant and subordinate under the heading of a single service, denoted by the relative term \mathit{s} for ^{\backprime\backprime} \text{servant of}\, \underline{~~~~}\, ^{\prime\prime}.  The terms of this unified service are given by the following equation.

\begin{array}{*{11}{c}} \mathit{s} & = & \mathrm{C} \!:\! \mathrm{O} & +\!\!, & \mathrm{E} \!:\! \mathrm{D} & +\!\!, & \mathrm{I} \!:\! \mathrm{O} & +\!\!, & \mathrm{J} \!:\! \mathrm{D} & +\!\!, & \mathrm{J} \!:\! \mathrm{O} \end{array}

The inclusion of \mathrm{I} \!:\! \mathrm{C} under \mathit{s} might be implied by the plot of the play but since it is so hotly arguable I will leave it out of the toll.

One thing more we need to watch out for:  There are different conventions in the field regarding the ordering of terms in their applications and different conventions are more convenient under different circumstances, so there’s little chance any one of them can be canonized once and for all.  In our current reading we apply relative terms from right to left and our conception of relative multiplication, or relational composition, needs to be adjusted accordingly.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 8.2

Posted on February 18, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 8.2

I continue with my commentary on CP 3.73, developing the Othello example as a way of illustrating Peirce’s formalism.

In the development of the story so far, we have a universe of discourse characterized by the following equations:

\begin{array}{*{15}{c}} \mathbf{1} & = & \mathrm{B} & +\!\!, & \mathrm{C} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \\[6pt] \mathrm{b} & = & \mathrm{O} \\[6pt] \mathrm{m} & = & \mathrm{C} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \\[6pt] \mathrm{w} & = & \mathrm{B} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} \end{array}

This much forms a basis for the collection of absolute terms to be used in this example.  Let us now consider how we might represent an exemplary collection of relative terms.

Consider the genesis of relative terms, for example:

\begin{array}{l} ^{\backprime\backprime}\, \text{lover of}\, \underline{~~~~}\, ^{\prime\prime} \\[6pt] ^{\backprime\backprime}\, \text{betrayer to}\, \underline{~~~~}\, \text{of}\, \underline{~~~~}\, ^{\prime\prime} \\[6pt] ^{\backprime\backprime}\, \text{winner over of}\, \underline{~~~~}\, \text{to}\, \underline{~~~~}\, \text{from}\, \underline{~~~~}\, ^{\prime\prime} \end{array}

We may regard these fill-in-the-blank forms as being derived by a kind of rhematic abstraction from the corresponding instances of absolute terms.

The following examples illustrate the relationships that exist among absolute terms, relative terms, relations, and elementary relations.

  • The relative term ^{\backprime\backprime} \text{lover of}\, \underline{~~~~}\, ^{\prime\prime} can be derived from the absolute term ^{\backprime\backprime} \text{lover of Emilia} ^{\prime\prime} by removing the absolute term ^{\backprime\backprime} \text{Emilia} ^{\prime\prime}.

    Iago is a lover of Emilia, so the relate-correlate pair \mathrm{I} \!:\! \mathrm{E} is an element of the dyadic relation associated with the relative term ^{\backprime\backprime} \text{lover of}\, \underline{~~~~}\, ^{\prime\prime}.

  • The relative term ^{\backprime\backprime} \text{betrayer to}\, \underline{~~~~}\, \text{of}\, \underline{~~~~}\, ^{\prime\prime} can be derived from the absolute term ^{\backprime\backprime} \text{betrayer to Othello of Desdemona} ^{\prime\prime} by removing the absolute terms ^{\backprime\backprime} \text{Othello} ^{\prime\prime} and ^{\backprime\backprime} \text{Desdemona} ^{\prime\prime}.

    Iago is a betrayer to Othello of Desdemona, so the relate-correlate-correlate triple \mathrm{I} \!:\! \mathrm{O} \!:\! \mathrm{D} is an element of the triadic relation associated with the relative term ^{\backprime\backprime} \text{betrayer to}\, \underline{~~~~}\, \text{of}\, \underline{~~~~}\, ^{\prime\prime}.

  • The relative term ^{\backprime\backprime} \text{winner over of}\, \underline{~~~~}\, \text{to}\, \underline{~~~~}\, \text{from}\, \underline{~~~~}\, ^{\prime\prime} can be derived from the absolute term ^{\backprime\backprime} \text{winner over of Othello to Iago from Cassio} ^{\prime\prime} by removing the absolute terms ^{\backprime\backprime} \text{Othello} ^{\prime\prime}, ^{\backprime\backprime} \text{Iago} ^{\prime\prime}, and ^{\backprime\backprime} \text{Cassio} ^{\prime\prime}.

    Iago is a winner over of Othello to Iago from Cassio, so the elementary relative term \mathrm{I} \!:\! \mathrm{O} \!:\! \mathrm{I} \!:\! \mathrm{C} is an element of the tetradic relation associated with the relative term ^{\backprime\backprime} \text{winner over of}\, \underline{~~~~}\, \text{to}\, \underline{~~~~}\, \text{from}\, \underline{~~~~}\, ^{\prime\prime}.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments