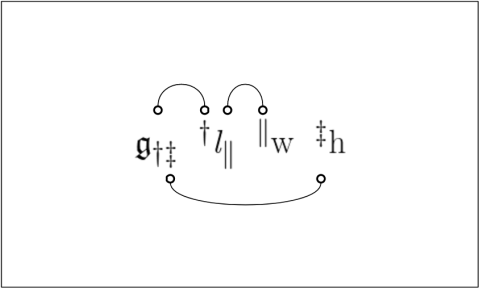
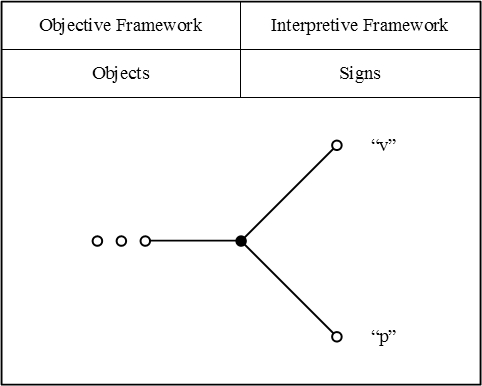
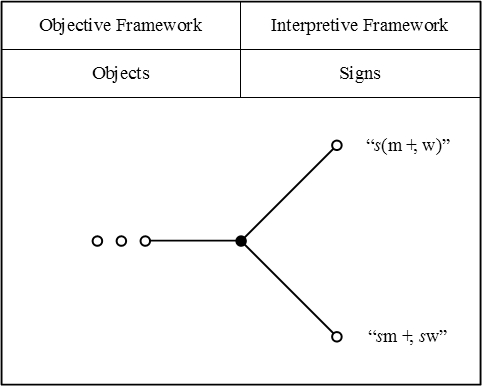
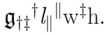Peirce’s 1870 “Logic of Relatives” • Comment 8.1

Posted on February 18, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 8.1

To my way of thinking, CP 3.73 is one of the most remarkable passages in the history of logic.  In this first pass over its deeper contents I won’t be able to accord it much more than a superficial dusting off.

Let us invent a concrete example to illustrate the use of Peirce’s notation.  Imagine a discourse whose universe X will remind us of the cast of characters in Shakespeare’s Othello.

X ~=~ \{ \text{Bianca}, \text{Cassio}, \text{Clown}, \text{Desdemona}, \text{Emilia}, \text{Iago}, \text{Othello} \}

The universe X is “that class of individuals about which alone the whole discourse is understood to run” but its marking out for special recognition as a universe of discourse in no way rules out the possibility that “discourse may run upon something which is not a subjective part of the universe;  for instance, upon the qualities or collections of the individuals it contains” (CP 3.65).

In order to afford ourselves the convenience of abbreviated terms while preserving Peirce’s conventions about capitalization, we may use the alternate terms {}^{\backprime\backprime}\mathrm{u} {}^{\prime\prime} for the universe X and {}^{\backprime\backprime} \mathrm{Jeste} {}^{\prime\prime} for the character \text{Clown}.  This permits the above description of the universe of discourse to be rewritten in the following fashion.

\mathrm{u} ~=~ \{ \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}, \mathrm{I}, \mathrm{J}, \mathrm{O} \}

This specification of the universe of discourse could be summed up in Peirce’s notation by the following equation.

\begin{array}{*{15}{c}} \mathbf{1} & = & \mathrm{B} & +\!\!, & \mathrm{C} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \end{array}

Within this discussion, then, the individual terms are as follows.

\begin{array}{*{7}{c}} ^{\backprime\backprime}\mathrm{B}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{C}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{D}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{E}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{I}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{J}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{O}^{\prime\prime} \end{array}

Each of these terms denotes in a singular fashion the corresponding individual in X.

By way of general terms in this discussion, we may begin with the following set.

\begin{array}{ccl} ^{\backprime\backprime}\mathrm{b}^{\prime\prime} & = & ^{\backprime\backprime}\mathrm{black}^{\prime\prime} \\[6pt] ^{\backprime\backprime}\mathrm{m}^{\prime\prime} & = & ^{\backprime\backprime}\mathrm{man}^{\prime\prime} \\[6pt] ^{\backprime\backprime}\mathrm{w}^{\prime\prime} & = & ^{\backprime\backprime}\mathrm{woman}^{\prime\prime} \end{array}

The denotation of a general term may be given by means of an equation between terms.

\begin{array}{*{15}{c}} \mathrm{b} & = & \mathrm{O} \\[6pt] \mathrm{m} & = & \mathrm{C} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \\[6pt] \mathrm{w} & = & \mathrm{B} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} \end{array}

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 8

Posted on February 17, 2014 by Jon Awbrey

We continue with §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 8

The Signs for Multiplication (cont.)

Thus far, we have considered the multiplication of relative terms only.  Since our conception of multiplication is the application of a relation, we can only multiply absolute terms by considering them as relatives.

Now the absolute term “man” is really exactly equivalent to the relative term “man that is ──”, and so with any other.  I shall write a comma after any absolute term to show that it is so regarded as a relative term.

Then “man that is black” will be written:

\mathrm{m},\!\mathrm{b}.

But not only may any absolute term be thus regarded as a relative term, but any relative term may in the same way be regarded as a relative with one correlate more.  It is convenient to take this additional correlate as the first one.

Then:

\mathit{l},\!\mathit{s}\mathrm{w}

will denote a lover of a woman that is a servant of that woman.

The comma here after \mathit{l} should not be considered as altering at all the meaning of \mathit{l}\,, but as only a subjacent sign, serving to alter the arrangement of the correlates.

In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates.

So:

\mathrm{m},\!,\!\mathrm{b},\!\mathrm{r}

interpreted like

\mathfrak{g}\mathit{o}\mathrm{h}

means a man that is a rich individual and is a black that is that rich individual.

But this has no other meaning than:

\mathrm{m},\!\mathrm{b},\!\mathrm{r}

or a man that is a black that is rich.

Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number.

If, therefore, \mathit{l},\!,\!\mathit{s}\mathrm{w} is not the same as \mathit{l},\!\mathit{s}\mathrm{w} (as it plainly is not, because the latter means a lover and servant of a woman, and the former a lover of and servant of and same as a woman), this is simply because the writing of the comma alters the arrangement of the correlates.

And if we are to suppose that absolute terms are multipliers at all (as mathematical generality demands that we should), we must regard every term as being a relative requiring an infinite number of correlates to its virtual infinite series “that is ── and is ── and is ── etc.”

Now a relative formed by a comma of course receives its subjacent numbers like any relative, but the question is, What are to be the implied subjacent numbers for these implied correlates?

Any term may be regarded as having an infinite number of factors, those at the end being ones, thus:

\mathit{l},\!\mathit{s}\mathrm{w} ~=~ \mathit{l},\!\mathit{s}\mathrm{w},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1}, ~\text{etc.}

A subjacent number may therefore be as great as we please.

But all these ones denote the same identical individual denoted by \mathrm{w} ;  what then can be the subjacent numbers to be applied to \mathit{s} , for instance, on account of its infinite “that is” ’s?  What numbers can separate it from being identical with \mathrm{w} ?  There are only two.  The first is zero, which plainly neutralizes a comma completely, since

\mathit{s},_0\!\mathrm{w} ~=~ \mathit{s}\mathrm{w}

and the other is infinity;  for as 1^\infty is indeterminate in ordinary algebra, so it will be shown hereafter to be here, so that to remove the correlate by the product of an infinite series of ones is to leave it indeterminate.

Accordingly,

\mathrm{m},_\infty

should be regarded as expressing some man.

Any term, then, is properly to be regarded as having an infinite number of commas, all or some of which are neutralized by zeros.

“Something” may then be expressed by:

\mathit{1}_\infty.

I shall for brevity frequently express this by an antique figure one (\mathfrak{1}).

“Anything” by:

\mathit{1}_0.

I shall often also write a straight 1 for anything.

(Peirce, CP 3.73)

References

  • Peirce, C.S. (1870), “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole’s Calculus of Logic”, Memoirs of the American Academy of Arts and Sciences 9, 317–378, 26 January 1870.  Reprinted, Collected Papers 3.45–149, Chronological Edition 2, 359–429.  Online (1) (2) (3).
  • Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958.
  • Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 21 Comments

Peirce’s 1870 “Logic of Relatives” • Proto-Graphical Syntax

Posted on February 12, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Proto-Graphical Syntax

It is clear from our last Selection that Peirce is already on the verge of a graphical syntax for the logic of relative terms.  Indeed, it is likely he had already reached that point in his own thinking some time before.

For instance, it seems quite impossible for a person with any graphical sensitivity whatever to scan that last variation on “giver of a horse to a lover of a woman” without drawing or at least imagining lines of identity to connect the corresponding marks of reference, as shown in the following Figure.

Giver of a Horse to a Lover of a Woman

\text{Figure 3. Giver of a Horse to a Lover of a Woman}

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 12 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 7

Posted on February 7, 2014 by Jon Awbrey

We continue with §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 7

The Signs for Multiplication (cont.)

The associative principle does not hold in this counting of factors.  Because it does not hold, these subjacent numbers are frequently inconvenient in practice, and I therefore use also another mode of showing where the correlate of a term is to be found.  This is by means of the marks of reference, \dagger\, \ddagger\, \parallel\, \S\, \P, which are placed subjacent to the relative term and before and above the correlate.  Thus, giver of a horse to a lover of a woman may be written:

Giver of a Horse to a Lover of a Woman

The asterisk I use exclusively to refer to the last correlate of the last relative of the algebraic term.

Now, considering the order of multiplication to be: — a term, a correlate of it, a correlate of that correlate, etc. — there is no violation of the associative principle.  The only violations of it in this mode of notation are that in thus passing from relative to correlate, we skip about among the factors in an irregular manner, and that we cannot substitute in such an expression as \mathfrak{g}\mathit{o}\mathrm{h} a single letter for \mathit{o}\mathrm{h}.

I would suggest that such a notation may be found useful in treating other cases of non‑associative multiplication.  By comparing this with what was said above [CP 3.55] concerning functional multiplication, it appears that multiplication by a conjugative term is functional, and that the letter denoting such a term is a symbol of operation.  I am therefore using two alphabets, the Greek and [Gothic], where only one was necessary.  But it is convenient to use both.

(Peirce, CP 3.71–72)

References

  • Peirce, C.S. (1870), “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole’s Calculus of Logic”, Memoirs of the American Academy of Arts and Sciences 9, 317–378, 26 January 1870.  Reprinted, Collected Papers 3.45–149, Chronological Edition 2, 359–429.  Online (1) (2) (3).
  • Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958.
  • Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Semiotics, Triadicity, Visualization | Tagged , , , , , , , | 11 Comments

Peirce’s 1870 “Logic of Relatives” • Sets as Sums

Posted on February 6, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Sets as Sums

Peirce’s way of representing sets as logical sums may seem arcane, but it’s quite often used in mathematics and remains the tool of choice in many branches of algebra, combinatorics, computing, and statistics to this day.

Peirce applied this genre of representation to logic in fairly novel ways and the degree to which he elaborated its use in the logic of relative terms is certainly original with him, but this particular device, going under the handle of generating functions, goes way back, well before anyone thought of sticking a flag in set theory as a separate territory or of trying to fence off our native possessions of classes and collections with explicit decrees of axioms.  And back in the days when a computer was simply a person who computed, well before the advent of electronic computers we take for granted today, mathematicians commonly used generating functions as a rough and ready sort of addressable memory to organize, store, and keep track of their accounts on a wide variety of formal objects.

Let’s look at a few simple examples of generating functions, much as I encountered them during my own first adventures in the Realm of Combinatorics.

Suppose we are given a set of three elements, say, \{ a, b, c \}, and we are asked to find all the ways of choosing a subset from this collection.

We can represent the problem setup as the problem of computing the following product:

(1 + a)(1 + b)(1 + c).

The factor (1 + a) represents the option we have, in choosing a subset of \{ a, b, c \}, to exclude the element a (signified by the 1), or else to include it (signified by the a), proceeding in a similar fashion with the other elements in their turn.

Probably on account of all those years I flippered away playing the oldtime pinball machines, I tend to imagine a product like that being displayed in a vertical array:

\begin{matrix} (1 ~+~ a) \\ (1 ~+~ b) \\ (1 ~+~ c) \end{matrix}

I picture that as a playboard with six bumpers, the ball chuting down the board in such a way as to strike exactly one of the two bumpers on each of the three levels.

So a trajectory of the ball where it hits the a bumper on the 1st level, hits the 1 bumper on the 2nd level, hits the c bumper on the 3rd level, and then exits the board, represents a single term in the desired product and corresponds to the subset \{ a, c \}.

Multiplying out the product (1 + a)(1 + b)(1 + c), one obtains the sum:

\begin{array}{*{15}{c}} 1 & + & a & + & b & + & c & + & ab & + & ac & + & bc & + & abc. \end{array}

This informs us that the subsets of choice are:

\begin{matrix} \varnothing, & \{a\}, & \{b\}, & \{c\}, & \{a, b\}, & \{a, c\}, & \{b, c\}, & \{a, b, c\}. \end{matrix}

And so they are.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Semiotics, Triadicity, Visualization | Tagged , , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 6

Posted on February 5, 2014 by Jon Awbrey

We continue with §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 6

The application of a relation is one of the most basic operations in Peirce’s logic.  Because relation applications are so pervasive and because Peirce treats them on the pattern of algebraic multiplication, the part of §3 concerned with “The Signs for Multiplication” will occupy our attention for many days to come.

The Signs for Multiplication (cont.)

A conjugative term like giver naturally requires two correlates, one denoting the thing given, the other the recipient of the gift.

We must be able to distinguish, in our notation, the giver of \mathrm{A} to \mathrm{B} from the giver to \mathrm{A} of \mathrm{B}, and, therefore, I suppose the signification of the letter equivalent to such a relative to distinguish the correlates as first, second, third, etc., so that “giver of ── to ──” and “giver to ── of ──” will be expressed by different letters.

Let \mathfrak{g} denote the latter of these conjugative terms.  Then, the correlates or multiplicands of this multiplier cannot all stand directly after it, as is usual in multiplication, but may be ranged after it in regular order, so that:

\mathfrak{g}\mathit{x}\mathit{y}

will denote a giver to \mathit{x} of \mathit{y}.

But according to the notation, \mathit{x} here multiplies \mathit{y}, so that if we put for \mathit{x} owner (\mathit{o}), and for \mathit{y} horse (\mathrm{h}),

\mathfrak{g}\mathit{o}\mathrm{h}

appears to denote the giver of a horse to an owner of a horse.  But let the individual horses be \mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}, ~\text{etc.}

Then:

\mathrm{h} ~=~ \mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!, ~\text{etc.}

\mathfrak{g}\mathit{o}\mathrm{h} ~=~ \mathfrak{g}\mathit{o}(\mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}) ~=~ \mathfrak{g}\mathit{o}\mathrm{H} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime\prime} ~+\!\!, ~\text{etc.}

Now this last member must be interpreted as a giver of a horse to the owner of that horse, and this, therefore must be the interpretation of \mathfrak{g}\mathit{o}\mathrm{h}.  This is always very important.  A term multiplied by two relatives shows that the same individual is in the two relations.

If we attempt to express the giver of a horse to a lover of a woman, and for that purpose write:

\mathfrak{g}\mathit{l}\mathrm{w}\mathrm{h},

we have written giver of a woman to a lover of her, and if we add brackets, thus,

\mathfrak{g}(\mathit{l}\mathrm{w})\mathrm{h},

we abandon the associative principle of multiplication.

A little reflection will show that the associative principle must in some form or other be abandoned at this point.  But while this principle is sometimes falsified, it oftener holds, and a notation must be adopted which will show of itself when it holds.  We already see that we cannot express multiplication by writing the multiplicand directly after the multiplier;  let us then affix subjacent numbers after letters to show where their correlates are to be found.  The first number shall denote how many factors must be counted from left to right to reach the first correlate, the second how many more must be counted to reach the second, and so on.

Then, the giver of a horse to a lover of a woman may be written:

\mathfrak{g}_{12} \mathit{l}_1 \mathrm{w} \mathrm{h} ~=~ \mathfrak{g}_{11} \mathit{l}_2 \mathrm{h} \mathrm{w} ~=~ \mathfrak{g}_{2(-1)} \mathrm{h} \mathit{l}_1 \mathrm{w}.

Of course a negative number indicates that the former correlate follows the latter by the corresponding positive number.

A subjacent zero makes the term itself the correlate.

Thus,

\mathit{l}_0

denotes the lover of that lover or the lover of himself, just as \mathfrak{g}\mathit{o}\mathrm{h} denotes that the horse is given to the owner of itself, for to make a term doubly a correlate is, by the distributive principle, to make each individual doubly a correlate, so that:

\mathit{l}_0 ~=~ \mathit{L}_0 ~+\!\!,~ \mathit{L}_0^{\prime} ~+\!\!,~ \mathit{L}_0^{\prime\prime} ~+\!\!,~ \text{etc.}

A subjacent sign of infinity may indicate that the correlate is indeterminate, so that:

\mathit{l}_\infty

will denote a lover of something.  We shall have some confirmation of this presently.

If the last subjacent number is a one it may be omitted.  Thus we shall have:

\mathit{l}_1 ~=~ \mathit{l},

\mathfrak{g}_{11} ~=~ \mathfrak{g}_1 ~=~ \mathfrak{g}.

This enables us to retain our former expressions \mathit{l}\mathrm{w}, \mathfrak{g}\mathit{o}\mathrm{h}, ~\text{etc.}

(Peirce, CP 3.69–70)

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Semiotics, Triadicity, Visualization | Tagged , , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 5

Posted on February 4, 2014 by Jon Awbrey

On to the next part of §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 5

The Signs for Multiplication

I shall adopt for the conception of multiplication the application of a relation, in such a way that, for example, \mathit{l}\mathrm{w} shall denote whatever is lover of a woman.  This notation is the same as that used by Mr. De Morgan, although he appears not to have had multiplication in his mind.

\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w}) will, then, denote whatever is servant of anything of the class composed of men and women taken together.  So that:

\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w}) ~=~ \mathit{s}\mathrm{m} ~+\!\!,~ \mathit{s}\mathrm{w}.

(\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w} will denote whatever is lover or servant to a woman, and:

(\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w} ~=~ \mathit{l}\mathrm{w} ~+\!\!,~ \mathit{s}\mathrm{w}.

(\mathit{s}\mathit{l})\mathrm{w} will denote whatever stands to a woman in the relation of servant of a lover, and:

(\mathit{s}\mathit{l})\mathrm{w} ~=~ \mathit{s}(\mathit{l}\mathrm{w}).

Thus all the absolute conditions of multiplication are satisfied.

The term “identical with ──” is a unity for this multiplication.  That is to say, if we denote “identical with ──” by \mathit{1} we have:

x \mathit{1} ~=~ x ~ ,

whatever relative term x may be.  For what is a lover of something identical with anything, is the same as a lover of that thing.

(Peirce, CP 3.68)

Peirce in 1870 is five years down the road from the Peirce of 1865–1866 who lectured extensively on the role of sign relations in the logic of scientific inquiry, articulating their involvement in the three types of inference, and inventing the concept of “information” to explain what it is that signs convey in the process.  By this time, then, the semiotic or sign relational approach to logic is so implicit in his way of working that he does not always take the trouble to point out its distinctive features at each and every turn.  So let’s take a moment to draw out a few of those characters.

Sign relations, like any brand of non-trivial triadic relations, can become overwhelming to think about once the cardinality of the object, sign, and interpretant domains or the complexity of the relation itself ascends beyond the simplest examples.  Furthermore, most of the strategies we’d normally use to control the complexity, like neglecting one of the domains, in effect, projecting the triadic sign relation onto one of its dyadic faces, or focusing on a single ordered triple (o, s, i) at a time, can result in our receiving a distorted impression of the sign relation’s true nature and structure.

I find it helps me to draw, or at least to imagine drawing, diagrams of the following form, where I can keep tabs on what’s an object, what’s a sign, and what’s an interpretant sign, for a selected set of sign-relational triples.

Figure 1 shows how I would picture Peirce’s example of equivalent terms, \mathrm{v} = \mathrm{p}, where ``\mathrm{v}" denotes the Vice-President of the United States, and ``\mathrm{p}" denotes the President of the Senate of the United States.

Equivalent Terms v = p

\text{Figure 1. Equivalent Terms}~ ``\mathrm{v}" = ``\mathrm{p}"

Depending on whether we interpret the terms ``\mathrm{v}" and ``\mathrm{p}" as applying to persons who hold the offices at one particular time or as applying to all persons who have held the offices over an extended period of history, their denotations may be either singular of plural, respectively.

Terms referring to many objects are known as having general denotations or plural referents.  They may be represented in the above style of picture by drawing an ellipsis of three nodes like “o o o” at the object ends of sign relational triples.

For a more complicated example, Figure 2 shows how I would picture Peirce’s example of an equivalence between terms which comes about by applying the distributive law for relative multiplication over absolute summation.

Equivalent Terms s(m +, w) = sm +, sw

\text{Figure 2. Equivalent Terms}~ ``\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w})" = ``\mathit{s}\mathrm{m} ~+\!\!,~ \mathit{s}\mathrm{w}"

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Semiotics, Triadicity, Visualization | Tagged , , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 4

Posted on January 31, 2014 by Jon Awbrey

Here is the next part of §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 4

The Signs for Addition

The sign of addition is taken by Boole so that

x + y

denotes everything denoted by x, and, besides, everything denoted by y.

Thus

\mathrm{m} + \mathrm{w}

denotes all men, and, besides, all women.

This signification for this sign is needed for connecting the notation of logic with that of the theory of probabilities.  But if there is anything which is denoted by both terms of the sum, the latter no longer stands for any logical term on account of its implying that the objects denoted by one term are to be taken besides the objects denoted by the other.

For example,

\mathrm{f} + \mathrm{u}

means all Frenchmen besides all violinists, and, therefore, considered as a logical term, implies that all French violinists are besides themselves.

For this reason alone, in a paper which is published in the Proceedings of the Academy for March 17, 1867, I preferred to take as the regular addition of logic a non-invertible process, such that

\mathrm{m} ~+\!\!,~ \mathrm{b}

stands for all men and black things, without any implication that the black things are to be taken besides the men;  and the study of the logic of relatives has supplied me with other weighty reasons for the same determination.

Since the publication of that paper, I have found that Mr. W. Stanley Jevons, in a tract called Pure Logic, or the Logic of Quality [1864], had anticipated me in substituting the same operation for Boole’s addition, although he rejects Boole’s operation entirely and writes the new one with a  +  sign while withholding from it the name of addition.

It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions.  But the notation has other recommendations.  The conception of taking together involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five.  Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive.

Addition being taken in this sense, nothing is to be denoted by zero, for then

x ~+\!\!,~ 0 ~=~ x

whatever is denoted by x;  and this is the definition of zero.  This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of zero and that of nothing, and because we shall thus have

[0] ~=~ 0.

(Peirce, CP 3.67)

A wealth of issues arises here I hope to take up in greater depth at a later point, but for the moment I shall be able to mention only the barest sample of them in passing.

The two papers preceding this one in CP 3 are Peirce’s papers of March and September 1867 in the Proceedings of the American Academy of Arts and Sciences, titled “On an Improvement in Boole’s Calculus of Logic” and “Upon the Logic of Mathematics”, respectively.  Among other things, these two papers provide us with further clues about the motivating considerations which brought Peirce to introduce the “number of a term” function, signified here by square brackets.  I have already quoted from the “Logic of Mathematics” paper in a related connection.  Here are the links to those excerpts:

In setting up a correspondence between “letters” and “numbers”, Peirce constructs a structure-preserving map from a logical domain to a numerical domain.  That he does this deliberately is evidenced by the care that he takes with the conditions under which the chosen aspects of structure are preserved, along with his recognition of the critical fact that zeroes are preserved by the mapping.

Incidentally, Peirce appears to have an inkling of the problems that would later be caused by using the plus sign for inclusive disjunction, but his advice was overridden by the dialects of applied logic which developed in various communities, retarding the exchange of information among engineering, mathematical, and philosophical specialties all throughout the subsequent century.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Semiotics, Triadicity, Visualization | Tagged , , , , , , , | 13 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 3

Posted on January 30, 2014 by Jon Awbrey

We move on to the next part of §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 3

The Signs of Inclusion, Equality, Etc.

I shall follow Boole in taking the sign of equality to signify identity.  Thus, if \mathrm{v} denotes the Vice-President of the United States, and \mathrm{p} the President of the Senate of the United States,

\mathrm{v} = \mathrm{p}

means that every Vice-President of the United States is President of the Senate, and every President of the United States Senate is Vice-President.

The sign “less than” is to be so taken that

\mathrm{f} < \mathrm{m}

means that every Frenchman is a man, but there are men besides Frenchmen.  Drobisch has used this sign in the same sense.  It will follow from these significations of  =  and  <  that the sign  -\!\!\!<  (or \leqq, “as small as”) will mean “is”.  Thus,

\mathrm{f} ~-\!\!\!< \mathrm{m}

means “every Frenchman is a man”, without saying whether there are any other men or not.  So,

\mathit{m} ~-\!\!\!< \mathit{l}

will mean that every mother of anything is a lover of the same thing;  although this interpretation in some degree anticipates a convention to be made further on.  These significations of  =  and  <  plainly conform to the indispensable conditions.  Upon the transitive character of these relations the syllogism depends, for by virtue of it, from

\mathrm{f} ~-\!\!\!< \mathrm{m}
and \mathrm{m} ~-\!\!\!< \mathrm{a}
we can infer that \mathrm{f} ~-\!\!\!< \mathrm{a}

that is, from every Frenchman being a man and every man being an animal, that every Frenchman is an animal.

But not only do the significations of  =  and  <  here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations.  Equality is, in fact, nothing but the identity of two numbers;  numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes.

So, to write 5 < 7 is to say that 5 is part of 7, just as to write \mathrm{f} < \mathrm{m} is to say that Frenchmen are part of men.  Indeed, if \mathrm{f} < \mathrm{m}, then the number of Frenchmen is less than the number of men, and if \mathrm{v} = \mathrm{p}, then the number of Vice-Presidents is equal to the number of Presidents of the Senate;  so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities.

(Peirce, CP 3.66)

The quantifier mapping from terms to numbers that Peirce signifies by means of the square bracket notation [t] has one of its principal uses in providing a basis for the computation of frequencies, probabilities, and all the other statistical measures constructed from them, and thus in affording a “principle of correspondence” between probability theory and its limiting case in the forms of logic.

This brings us once again to the relativity of contingency and necessity, as one way of approaching necessity is through the avenue of probability, describing necessity as a probability of 1, but the whole apparatus of probability theory only figures in if it is cast against the backdrop of probability space axioms, the reference class of distributions, and the sample space that we cannot help but abduce on the scene of observations.  Aye, there’s the snake eyes.  And with them we can see that there is always an irreducible quantum of facticity to all our necessities.  More plainly spoken, it takes a fairly complex conceptual infrastructure just to begin speaking of probabilities, and this setting can only be set up by means of abductive, fallible, hypothetical, and inherently risky mental acts.

Pragmatic thinking is the logic of abduction, which is another way of saying it addresses the question:  What may be hoped?  We have to face the possibility it may be just as impossible to speak of absolute identity with any hope of making practical philosophical sense as it is to speak of absolute simultaneity with any hope of making operational physical sense.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Semiotics, Triadicity, Visualization | Tagged , , , , , , , | 12 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 2

Posted on January 29, 2014 by Jon Awbrey

We continue with §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 2

Numbers Corresponding to Letters

I propose to use the term “universe” to denote that class of individuals about which alone the whole discourse is understood to run.  The universe, therefore, in this sense, as in Mr. De Morgan’s, is different on different occasions.  In this sense, moreover, discourse may run upon something which is not a subjective part of the universe;  for instance, upon the qualities or collections of the individuals it contains.

I propose to assign to all logical terms, numbers;  to an absolute term, the number of individuals it denotes;  to a relative term, the average number of things so related to one individual.  Thus in a universe of perfect men (\mathrm{men}), the number of “tooth of” would be 32.  The number of a relative with two correlates would be the average number of things so related to a pair of individuals;  and so on for relatives of higher numbers of correlates.  I propose to denote the number of a logical term by enclosing the term in square brackets, thus, [t].

(Peirce, CP 3.65)

Peirce’s remarks at CP 3.65 are so replete with remarkable ideas, some of them so taken for granted in mathematical discourse as usually to escape explicit mention, others so suggestive of things to come in a future remote from his time of writing, and yet so smoothly slipped into the stream of thought that it’s all too easy to overlook their significance — that all I can do to highlight their impact is to dress them up in different words, whose main advantage is being more jarring to the mind’s sensibilities.

  • Peirce’s mapping of letters to numbers, or logical terms to mathematical quantities, is the very core of what quantification theory is all about, definitely more to the point than the mere “innovation” of using distinctive symbols for the so-called quantifiers.
  • The mapping of logical terms to numerical measures, to express it in current language, would probably be recognizable as some kind of morphism or functor from a logical domain to a quantitative co-domain.
  • Notice that Peirce follows the mathematician’s usual practice, then and now, of making the status of being an individual or a universal relative to a discourse in progress.
  • It is worth noting that Peirce takes the plural denotation of terms for granted, or what’s the number of a term for, if it could not vary apart from being one or nil?
  • I also observe that Peirce takes the individual objects of a particular universe of discourse in a generative way, as opposed to a totalizing way, and thus these contingent individuals afford us with a basis for talking freely about collections, constructions, properties, qualities, subsets, and higher types built on them.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematics, Relation Theory, Semiotics, Triadicity, Visualization | Tagged , , , , , , , | 16 Comments