Cactus Language • Preliminaries 4

Posted on April 11, 2025 by Jon Awbrey

The informal mechanisms illustrated in the preceding discussion equip us with a description of cactus language adequate to providing conceptual and computational representations for the minimal formal logical system variously known as propositional logic or sentential calculus.

The painted cactus language \mathfrak{C} is actually a parameterized family of languages, consisting of one language \mathfrak{C}(\mathfrak{P}) for each set \mathfrak{P} of paints.

The alphabet \mathfrak{A} = \mathfrak{M} \cup \mathfrak{P} is the disjoint union of the following two sets of symbols.

\mathfrak{M} is the alphabet of markers, the set of punctuation marks, or the collection of syntactic constants common to all the languages \mathfrak{C}(\mathfrak{P}).  Various ways of representing the elements of \mathfrak{M} are shown in the following display.

Cactus Language Display 2

\mathfrak{P} is the palette, the alphabet of paints, or the collection of syntactic variables peculiar to the language \mathfrak{C}(\mathfrak{P}).  The set of signs in \mathfrak{P} may be enumerated as follows.

\mathfrak{P} = \{ \mathfrak{p}_j : j \in J \}.

Resources

cc: Academia.edu • BlueSky • Laws of Form • Mathstodon • Research Gate
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

This entry was posted in Automata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Differential Logic, Equational Inference, Formal Grammars, Formal Languages, Graph Theory, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Propositional Calculus, Visualization and tagged , , , , , , , , , , , , , , , , . Bookmark the permalink.

5 Responses to Cactus Language • Preliminaries 4

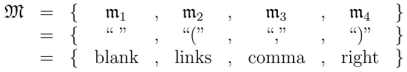
  1. Pingback: Survey of Animated Logical Graphs • 7 | Inquiry Into Inquiry

  2. Pingback: Survey of Animated Logical Graphs • 8 | Inquiry Into Inquiry

  3. ashkotin's avatar ashkotin says:
    May 10, 2025 at 4:56 am

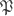    (disjoint union) This term is a little bit misleading as we see here and here. Maybe it’s better to say directly that \mathfrak{M} and \mathfrak{P} are disjointed?

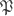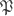    (\mathfrak{P} cardinality) It is more or less clear that J denotes a set of natural numbers without 0. But is it possible that \mathfrak{P} is infinite? Or maybe 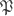\mathfrak{P} is mandatory infinite? This is unusual for the alphabet to be infinite and should be pointed out.

    Like

    Reply
    • Jon Awbrey's avatar Jon Awbrey says:
      May 10, 2025 at 8:40 am

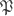      Actually, it’s \mathfrak{M} for markers or punctuation marks and \mathfrak{P} for paints.  Didn’t like using Fraktur but ran out of letters for the necessary distinctions.  Markers are just a set of four and Paints are a finite set intended to be interpreted eventually as boolean variables.  I think I said somewhere alphabets are finite sets but will go back and make sure that’s clear.

      Liked by 1 person

      Reply

  4. Pingback: Survey of Animated Logical Graphs • 8 | Systems Community of Inquiry

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.