Let’s stay with Peirce’s example of inductive inference a little longer and try to clear up the more troublesome confusions tending to arise.

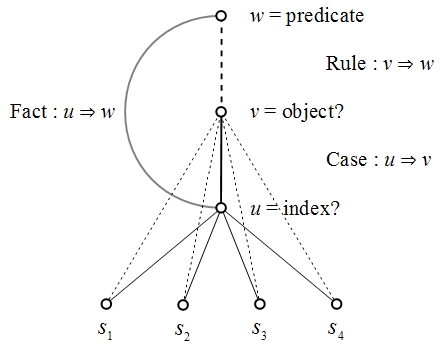
Figure 2 shows the implication ordering of logical terms in the form of a lattice diagram.

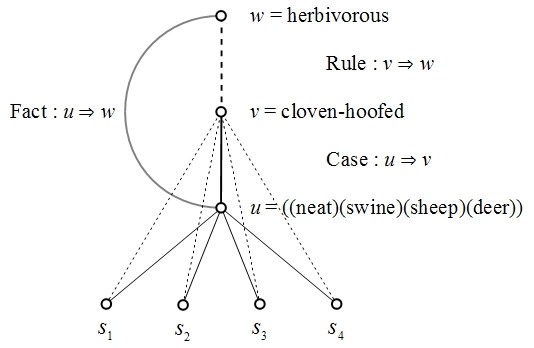
Figure 4 shows an inductive step of inquiry, as taken on the cue of an indicial sign.

One final point needs to be stressed.  It is important to recognize the disjunctive term itself — the syntactic formula “neat, swine, sheep, deer” or any logically equivalent formula — is not an index but a symbol.  It has the character of an artificial symbol which is constructed to fill a place in a formal system of symbols, for example, a propositional calculus.  In that setting it would normally be interpreted as a logical disjunction of four elementary propositions, denoting anything in the universe of discourse which has any of the four corresponding properties.

The artificial symbol “neat, swine, sheep, deer” denotes objects which serve as indices of the genus herbivore by virtue of their belonging to one of the four named species of herbivore.  But there is in addition a natural symbol which serves to unify the manifold of given species, namely, the concept of a cloven‑hoofed animal.

As a symbol or general representation, the concept of a cloven‑hoofed animal connotes an attribute and connotes it in such a way as to determine what it denotes.  Thus we observe a natural expansion in the connotation of the symbol, amounting to what Peirce calls the “superfluous comprehension”, the information added by an “ampliative” or synthetic inference.

In sum we have sufficient information to motivate an inductive inference, from the Fact and the Case to the Rule

Reference

• Peirce, C.S. (1866), “The Logic of Science, or, Induction and Hypothesis”, Lowell Lectures of 1866, pp. 357–504 in Writings of Charles S. Peirce : A Chronological Edition, Volume 1, 1857–1866, Peirce Edition Project, Indiana University Press, Bloomington, IN, 1982.

Resources

• This Blog • Survey of Pragmatic Semiotic Information
• OEIS Wiki • Information = Comprehension × Extension
• C.S. Peirce • Upon Logical Comprehension and Extension

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Inquiry Into Inquiry • Laws of Form • Ma^thstodon • Academia.edu
cc: Research Gate