Transformations of Logical Graphs • 11

Posted on May 15, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (8) • (9) • (10)

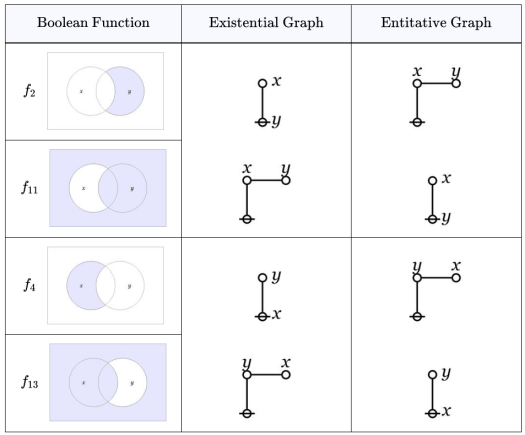
Continuing our scan of the Table in Episode 8, the next two orbits contain the logical graphs for the boolean functions f_{2}, f_{11}, f_{4}, f_{13}, in that order.  A first glance shows the two orbits have surprisingly intricate structures and relationships to each other — let’s isolate that section for a closer look.

\text{Interpretive Duality} \stackrel{_\bullet}{} \text{Subtractions and Implications}

Interpretive Duality • Subtractions and Implications

  • The boolean functions f_{2} and f_{4} are called subtraction functions.
  • The boolean functions f_{11} and f_{13} are called implication functions.
  • The logical graphs for f_{2} and f_{11} are dual to each other.
  • The logical graphs for f_{4} and f_{13} are dual to each other.

The values of the subtraction and implication functions for each (x, y) \in \mathbb{B} \times \mathbb{B} and the text expressions for their logical graphs are given in the following Table.

Subtractions and Implications

Resources

cc: FB | Logical Graphs • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

This entry was posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Interpretive Duality, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Visualization and tagged , , , , , , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.

4 Responses to Transformations of Logical Graphs • 11

  1. Pingback: Survey of Animated Logical Graphs • 7 | Inquiry Into Inquiry

  2. Pingback: Transformations of Logical Graphs • 12 | Inquiry Into Inquiry

  3. Pingback: Transformations of Logical Graphs • 13 | Inquiry Into Inquiry

  4. Pingback: Transformations of Logical Graphs • 14 | Inquiry Into Inquiry

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.