Transformations of Logical Graphs • 8

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6) • (7)

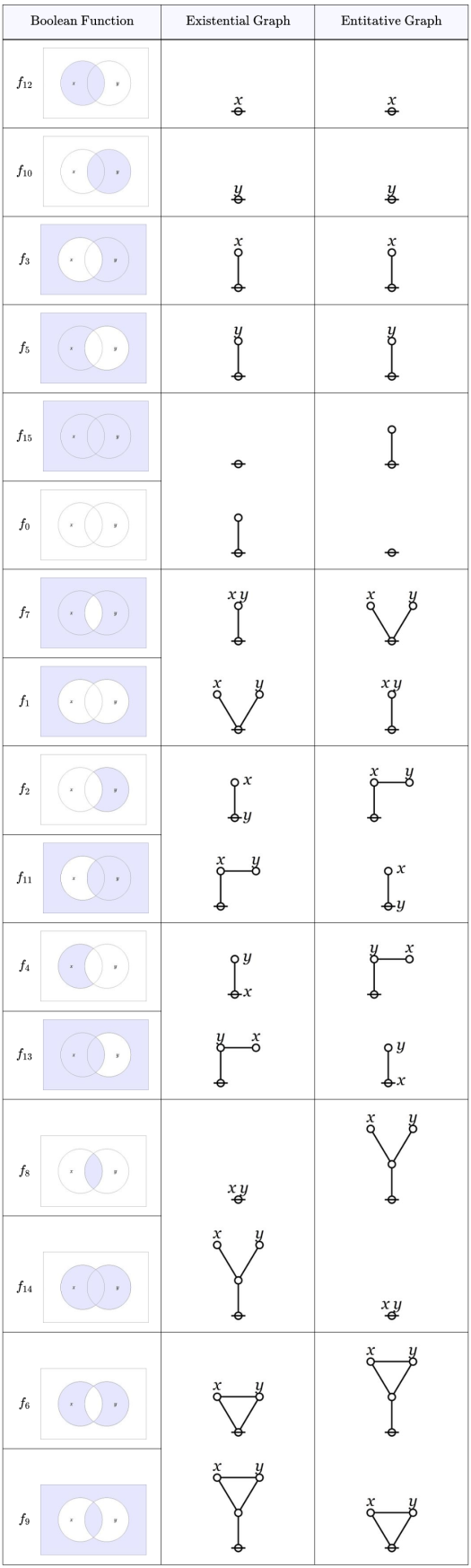
Turning again to our Table of Orbits let’s see what we can learn about the structure of the sign relational system in view.

As we saw in Episode 2, the transformation group $T = \{ 1, t \}$ partitions the set $X$ of 16 logical graphs and also the set $O$ of 16 boolean functions into 10 orbits, all together amounting to 4 singleton orbits and 6 doubleton orbits.

Points in singleton orbits are called fixed points of the transformation group $T : X \to X$ since they are left unchanged, or changed into themselves, by all group actions. Viewed in the frame of the sign relation $L \subseteq O \times X \times X,$ where the transformations in $T$ are literally translations in the linguistic sense, these $T$ -invariant graphs have the same denotations in $O$ for both Existential Interpreters and Entitative Interpreters.

$\text{Interpretive Duality as Sign Relation} \stackrel{_\bullet}{} \text{Orbit Order}$

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

	C.S. Peirce and Cate… on Survey of Precursors Of Catego…
	C.S. Peirce and Cate… on About
	Survey of Theme One… on Theme One Program • Jets and S…
	Theme One Program •… on Survey of Theme One Program •…
	Theme One Program •… on Theme One Program • Jets and S…
	Survey of Theme One… on Theme One Program • Jets and S…
	Theme One Program •… on Survey of Theme One Program •…
	Survey of Theme One… on Theme One Program • Exposition…
	Theme One Program •… on Survey of Theme One Program •…
	Theme One Program •… on Theme One Program • Exposition…

M	T	W	T	F	S	S
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31