Transformations of Logical Graphs • 7

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6)

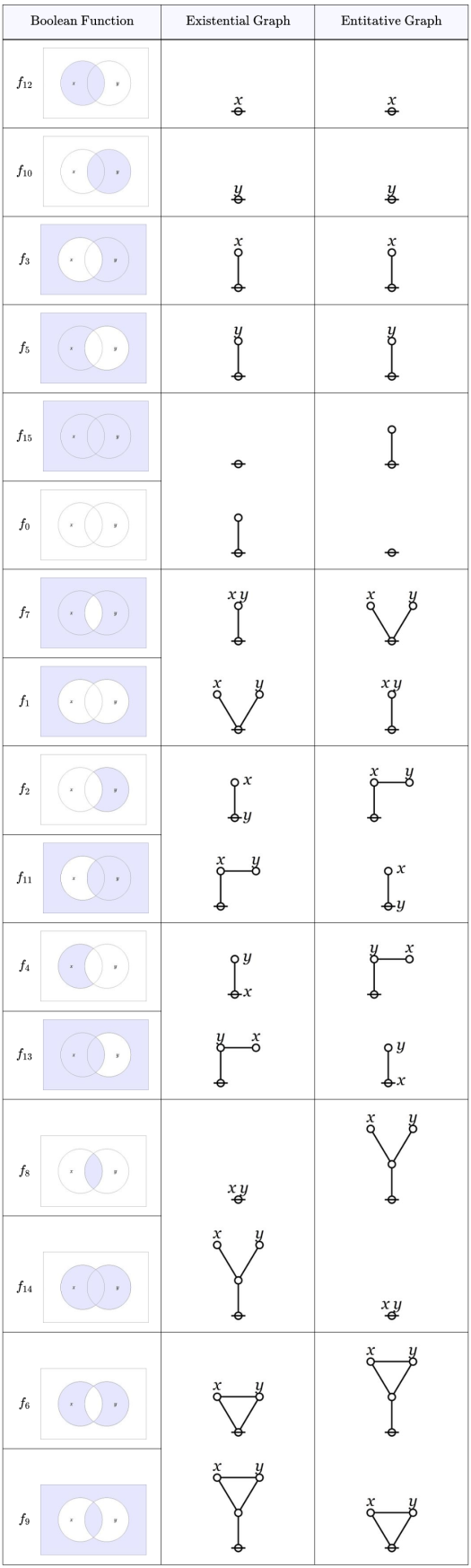
Our investigation has brought us to the point of seeing both a transformation group and a triadic sign relation in the duality between entitative and existential interpretations of logical graphs.

Given the level of the foregoing abstractions it helps to anchor them in concrete structural experience. In that spirit we’ve been pursuing the case of a group action $T : X \to X$ and a sign relation $L \subseteq O \times X \times X$ where $O$ is the set of boolean functions on two variables and $X$ is a set of logical graphs denoting those functions. We drew up a Table combining the aspects of both structures and sorted it according to the orbits $T$ induces on $X$ and consequently on $O.$

$\text{Interpretive Duality as Sign Relation} \stackrel{_\bullet}{} \text{Orbit Order}$

In the next few posts we’ll take up the orbits of logical graphs one by one, comparing and contrasting their syntax and semantics.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

	C.S. Peirce and Cate… on Survey of Precursors Of Catego…
	C.S. Peirce and Cate… on About
	Survey of Theme One… on Theme One Program • Jets and S…
	Theme One Program •… on Survey of Theme One Program •…
	Theme One Program •… on Theme One Program • Jets and S…
	Survey of Theme One… on Theme One Program • Jets and S…
	Theme One Program •… on Survey of Theme One Program •…
	Survey of Theme One… on Theme One Program • Exposition…
	Theme One Program •… on Survey of Theme One Program •…
	Theme One Program •… on Theme One Program • Exposition…

M	T	W	T	F	S	S
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31