Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5)

Our study of the duality between entitative and existential interpretations of logical graphs has brought to light its fully sign-relational character, casting the interpretive duality as a transformation of signs revolving about a common object domain.  The overall picture is a triadic relation linking an object domain with two sign domains, whose signs denote the objects in two distinct ways.

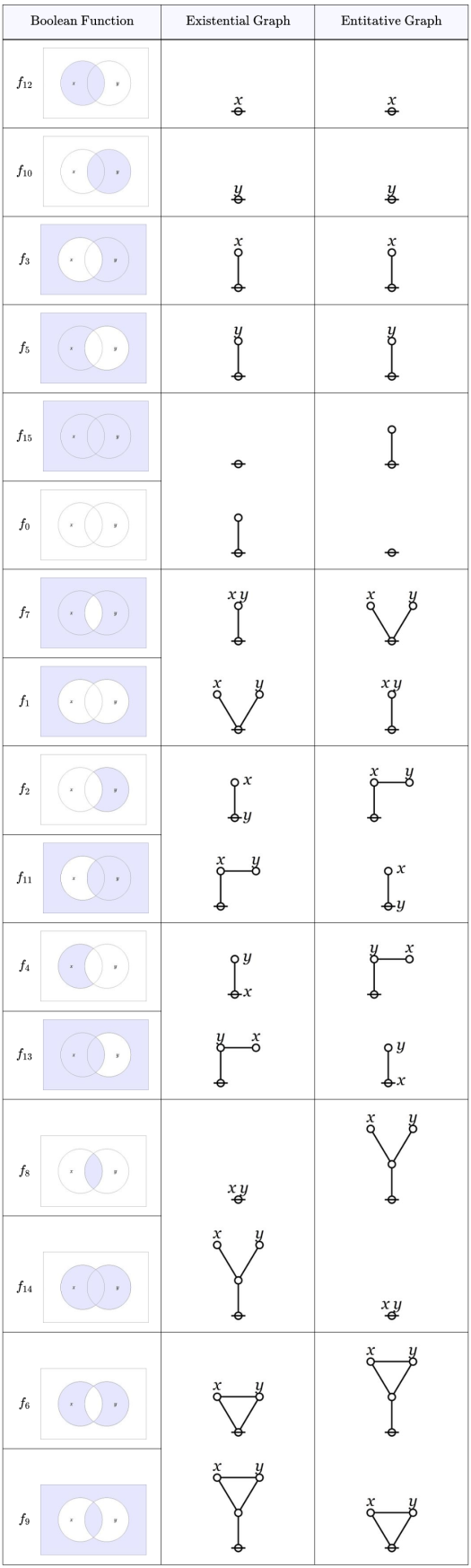
By way of constructing a concrete example, we let our object domain consist of the 16 boolean functions on 2 variables and we let our sign domains consist of representative logical graphs for those 16 functions.  Thus we arrived at the Table in the previous post, linked by its title below.

• Column 1 shows the object domain as the set of 16 boolean functions on 2 variables.
• Column 2 shows the sign domain as a representative set of logical graphs denoting the objects in according to the existential interpretation.
• Column 3 shows the interpretant domain as the same set of logical graphs denoting the objects in according to the entitative interpretation.

Additional aspects of the sign relation’s structure can be brought out by sorting the Table in accord with the orbits induced on the object domain by the group action inherent in the interpretive duality.  Performing that sort produces the following Table.

Resources

• Logic Syllabus
• Logical Graphs • First Impressions
• Logical Graphs • Formal Development
• Semeiotic • Sign Relations • Triadic Relations

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science