Differential Propositional Calculus • 33

Posted on December 27, 2023 by Jon Awbrey

Example 2. Drives and Their Vicissitudes (cont.)

Expressed in terms of drives and gears our next Example may be described as the family of 4^\text{th}‑gear curves in the fourth extension \mathrm{E}^4 X = \langle A, ~\mathrm{d}A, ~\mathrm{d}^2\!A, ~\mathrm{d}^3\!A, ~\mathrm{d}^4\!A \rangle.  Those are the trajectories generated subject to the dynamic law \mathrm{d}^4 A = 1, where it’s understood all higher order differences are equal to 0.

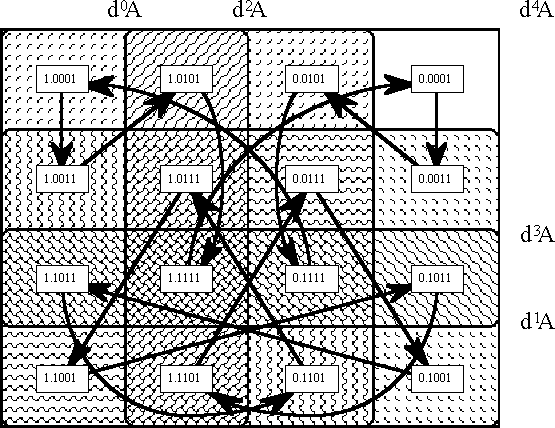
Since \mathrm{d}^4 A and all higher differences \mathrm{d}^k A are fixed, the state vectors vary only with respect to their projections as points of \mathrm{E}^3 X = \langle A, ~\mathrm{d}A, ~\mathrm{d}^2\!A, ~\mathrm{d}^3\!A \rangle.  Thus there is just enough space in a planar venn diagram to plot all the orbits and to show how they partition the points of \mathrm{E}^3 X.  It turns out there are exactly two possible orbits, of eight points each, as shown in the following Figure.

Example 2. Fourth Gear Orbits
\text{Example 2. Fourth Gear Orbits}

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

This entry was posted in Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Change, Computational Complexity, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamics, Dynamical Systems, Equational Inference, Functional Logic, Gradient Descent, Graph Theory, Group Theory, Hologrammautomaton, Indicator Functions, Logic, Logical Graphs, Mathematical Models, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Time, Visualization and tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.

2 Responses to Differential Propositional Calculus • 33

  1. Pingback: Survey of Differential Logic • 6 | Inquiry Into Inquiry

  2. Pingback: Survey of Differential Logic • 7 | Inquiry Into Inquiry

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.