Peirce’s Law • 5

Posted on October 23, 2023 by Jon Awbrey

Equational Form

A stronger form of Peirce’s law also holds, in which the final implication is observed to be reversible, resulting in the following equivalence.

((p \Rightarrow q) \Rightarrow p) \Leftrightarrow p

The converse implication p \Rightarrow ((p \Rightarrow q) \Rightarrow p) is clear enough on general principles, since p \Rightarrow (r \Rightarrow p) holds for any proposition r.

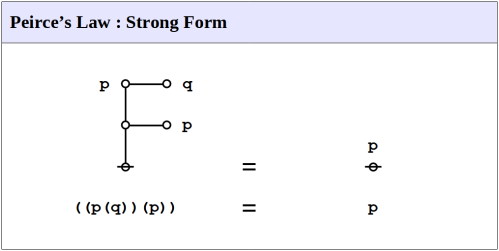
Representing propositions as logical graphs under the existential interpretation, the strong form of Peirce’s law is expressed by the following equation.

Peirce's Law : Strong Form

Reference

  • Peirce, Charles Sanders (1885), “On the Algebra of Logic : A Contribution to the Philosophy of Notation”, American Journal of Mathematics 7 (1885), 180–202.  Reprinted (CP 3.359–403), (CE 5, 162–190).

Resources

cc: FB | Logical Graphs • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

This entry was posted in C.S. Peirce, Equational Inference, Laws of Form, Logic, Logical Graphs, Mathematics, Peirce, Peirce's Law, Proof Theory, Propositional Calculus, Propositions As Types Analogy, Semiotics, Spencer Brown, Visualization and tagged , , , , , , , , , , , , , . Bookmark the permalink.