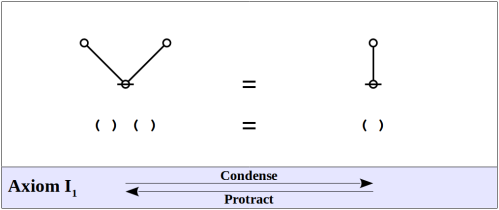
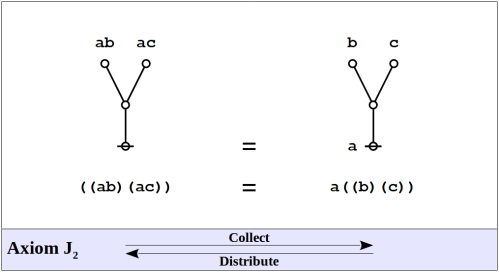
Axioms
The formal system of logical graphs is defined by a foursome of formal equations, called initials when regarded purely formally, in abstraction from potential interpretations, and called axioms when interpreted as logical equivalences. There are two arithmetic initials and two algebraic initials, as shown below.
Arithmetic Initials
Algebraic Initials
cc: FB | Logical Graphs • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
Inquiry Into Inquiry 
Pingback: Survey of Animated Logical Graphs • 5 | Inquiry Into Inquiry
Pingback: Survey of Animated Logical Graphs • 6 | Inquiry Into Inquiry
Pingback: Survey of Animated Logical Graphs • 7 | Inquiry Into Inquiry