Differential Propositional Calculus • 8

Posted on March 7, 2020 by Jon Awbrey

Differential Extensions

An initial universe of discourse A^\bullet supplies the groundwork for any number of further extensions, beginning with the first order differential extension \mathrm{E}A^\bullet.  The construction of \mathrm{E}A^\bullet can be described in the following stages.

  • The initial alphabet \mathfrak{A} = \{ ``a_1", \ldots, ``a_n" \} is extended by a first order differential alphabet \mathrm{d}\mathfrak{A} = \{ ``\mathrm{d}a_1", \ldots, ``\mathrm{d}a_n" \} resulting in a first order extended alphabet \mathrm{E}\mathfrak{A} defined as follows.

    \mathrm{E}\mathfrak{A} ~=~ \mathfrak{A} ~\cup~ \mathrm{d}\mathfrak{A} ~=~ \{ ``a_1", \ldots, ``a_n", ``\mathrm{d}a_1", \ldots, ``\mathrm{d}a_n" \}.

  • The initial basis \mathcal{A} = \{ a_1, \ldots, a_n \} is extended by a first order differential basis \mathrm{d}\mathcal{A} = \{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \} resulting in a first order extended basis \mathrm{E}\mathcal{A} defined as follows.

    \mathrm{E}\mathcal{A} ~=~ \mathcal{A} ~\cup~ \mathrm{d}\mathcal{A} ~=~ \{ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}.

  • The initial space A = \langle a_1, \ldots, a_n \rangle is extended by a first order differential space or tangent space \mathrm{d}A = \langle \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle at each point of A, resulting in a first order extended space or tangent bundle space \mathrm{E}A defined as follows.

    \mathrm{E}A ~=~ A ~\times~ \mathrm{d}A ~=~ \langle \mathrm{E}\mathcal{A} \rangle ~=~ \langle \mathcal{A} \cup \mathrm{d}\mathcal{A} \rangle ~=~ \langle a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle.

  • Finally, the initial universe A^\bullet = [ a_1, \ldots, a_n ] is extended by a first order differential universe or tangent universe \mathrm{d}A^\bullet = [ \mathrm{d}a_1, \ldots, \mathrm{d}a_n ] at each point of A^\bullet, resulting in a first order extended universe or tangent bundle universe \mathrm{E}A^\bullet defined as follows.

    \mathrm{E}A^\bullet ~=~ [ \mathrm{E}\mathcal{A} ] ~=~ [ \mathcal{A} ~\cup~ \mathrm{d}\mathcal{A} ] ~=~ [ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n ].

    This gives \mathrm{E}A^\bullet a type defined as follows.

    [ \mathbb{B}^n \times \mathbb{D}^n ] ~=~ (\mathbb{B}^n \times \mathbb{D}^n\ +\!\!\to \mathbb{B}) ~=~ (\mathbb{B}^n \times \mathbb{D}^n, \mathbb{B}^n \times \mathbb{D}^n \to \mathbb{B}).

A proposition in a differential extension of a universe of discourse is called a differential proposition and forms the analogue of a system of differential equations in ordinary calculus.  With these constructions, the first order extended universe \mathrm{E}A^\bullet and the first order differential propositions f : \mathrm{E}A \to \mathbb{B}, we arrive at the foothills of differential logic.

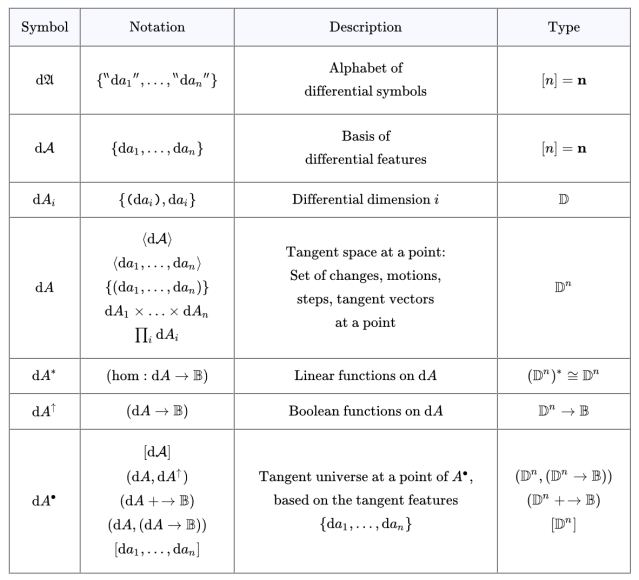
Table 11 summarizes the notations needed to describe the first order differential extensions of propositional calculi in a systematic manner.

\text{Table 11. Differential Extension} \stackrel{_\bullet}{} \text{Basic Notation}
Differential Extension • Basic Notation

Resources

cc: Cybernetics • Ontolog Forum • Peirce List • Structural Modeling • Systems Science

This entry was posted in Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Change, Computational Complexity, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamics, Dynamical Systems, Equational Inference, Functional Logic, Gradient Descent, Graph Theory, Group Theory, Hologrammautomaton, Indicator Functions, Logic, Logical Graphs, Mathematical Models, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Time, Visualization and tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.

4 Responses to Differential Propositional Calculus • 8

  1. Pingback: Survey of Differential Logic • 3 | Inquiry Into Inquiry

  2. Pingback: Survey of Differential Logic • 4 | Inquiry Into Inquiry

  3. Pingback: Survey of Differential Logic • 5 | Inquiry Into Inquiry

  4. Pingback: Survey of Differential Logic • 6 | Inquiry Into Inquiry

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.