Inquiry Into Inquiry

Differential Propositional Calculus • 22

Posted on December 14, 2023 by Jon Awbrey

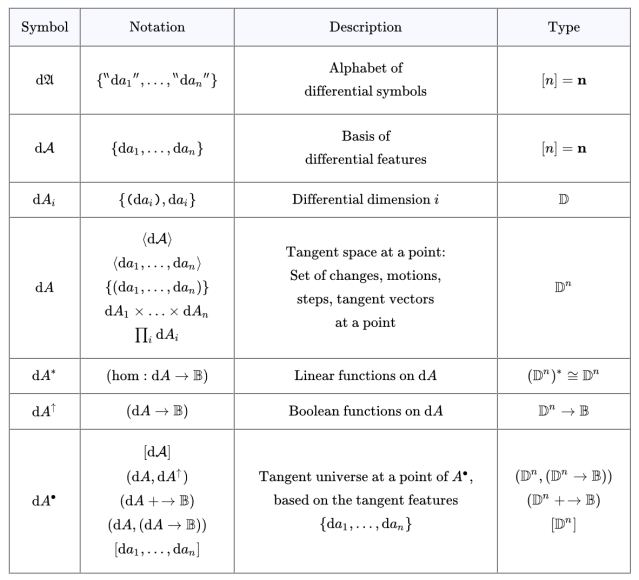
A One-Dimensional Universe (cont.)

The first order differential extension of $\mathcal{X}$ is $\mathrm{E}\mathcal{X} = \{ x_1, \mathrm{d}x_1 \} = \{ A, \mathrm{d}A \}.$ If the feature $A$ is interpreted as applying to some object or state then the feature $\mathrm{d}A$ may be taken as an attribute of the same object or state which tells it is changing significantly with respect to the property $A,$ as if it bore an “escape velocity” with respect to the state $A.$ In practice, differential features acquire their meaning through a class of temporal inference rules.

For example, relative to a frame of observation to be left implicit for now, if $A$ and $\mathrm{d}A$ are true at a given moment, it would be reasonable to assume $\texttt{(} A \texttt{)}$ will be true in the next moment of observation. Taken all together we have the fourfold scheme of inference shown below.

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Change, Computational Complexity, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamics, Dynamical Systems, Equational Inference, Functional Logic, Gradient Descent, Graph Theory, Group Theory, Hologrammautomaton, Indicator Functions, Logic, Logical Graphs, Mathematical Models, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Time, Visualization | Tagged Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Change, Computational Complexity, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamics, Dynamical Systems, Equational Inference, Functional Logic, Gradient Descent, Graph Theory, Group Theory, Hologrammautomaton, Indicator Functions, Logic, Logical Graphs, Mathematical Models, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Time, Visualization | 2 Comments

Differential Propositional Calculus • 21

Posted on December 12, 2023 by Jon Awbrey

There was never any more inception than there is now,
Nor any more youth or age than there is now;
And will never be any more perfection than there is now,
Nor any more heaven or hell than there is now.

— Walt Whitman • Leaves of Grass

A One‑Dimensional Universe

Let $\mathcal{X} = \{ A \}$ be a logical basis containing one boolean variable or logical feature $A.$ The basis element $A$ may be regarded as a simple proposition or coordinate projection $A : \mathbb{B} \to \mathbb{B}.$ Corresponding to the basis $\mathcal{X} = \{ A \}$ is the alphabet $\mathfrak{X} = \{ ``A" \}$ which serves whenever we need to make explicit mention of the symbols used in our formulas and representations.

The space $X = \langle A \rangle = \{ \texttt{(} A \texttt{)}, A \}$ of points (cells, vectors, interpretations) has cardinality $2^n = 2^1 = 2$ and is isomorphic to $\mathbb{B} = \{ 0, 1 \}.$ Moreover, $X$ may be identified with the set of singular propositions $\{ x : \mathbb{B} \xrightarrow{s} \mathbb{B} \}.$

The space of linear propositions $X^* = \{ \mathrm{hom} : \mathbb{B} \xrightarrow{\ell} \mathbb{B} \} = \{ 0, A \}$ is algebraically dual to $X$ and also has cardinality $2.$ Here, $``0"$ is interpreted as denoting the constant function $0 : \mathbb{B} \to \mathbb{B},$ amounting to the linear proposition of rank $0,$ while $A$ is the linear proposition of rank $1.$

Last but not least we have the positive propositions $\{ \mathrm{pos} : \mathbb{B} \xrightarrow{p} \mathbb{B} \} = \{ A, 1 \}$ of rank $1$ and $0,$ respectively, where $``1"$ is understood as denoting the constant function $1 : \mathbb{B} \to \mathbb{B}.$

All told there are $2^{2^n} = 2^{2^1} = 4$ propositions in the universe of discourse $\mathcal{X}^\bullet = [\mathcal{X}],$ collectively forming the set $X^\uparrow = \{ f : X \to \mathbb{B} \} = \{ 0, \texttt{(} A \texttt{)}, A, 1 \} \cong (\mathbb{B} \to \mathbb{B}).$

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

Differential Propositional Calculus • 20

Posted on December 11, 2023 by Jon Awbrey

I would have preferred to be enveloped in words, borne way beyond all possible beginnings.

— Michel Foucault • The Discourse on Language

Back to the Beginning • Exemplary Universes

To anchor our understanding of differential logic let’s look at how the various concepts apply in the simplest possible concrete cases, where the initial dimension is only 1 or 2. In spite of the simplicity of these cases it is possible to observe how central difficulties of the subject begin to arise already at this stage.

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

Differential Propositional Calculus • 19

Posted on December 10, 2023 by Jon Awbrey

Failing to fetch me at first keep encouraged,
Missing me one place search another,
I stop some where waiting for you

— Walt Whitman • Leaves of Grass

Life on Easy Street

The finite character of the extended universe $[\mathrm{E}\mathcal{A}]$ makes the task of solving differential propositions relatively straightforward. The solution set of the differential proposition $q : \mathrm{E}A \to \mathbb{B}$ is the set of models $q^{-1}(1)$ in $\mathrm{E}A.$ Finding all models of $q,$ the extended interpretations in $\mathrm{E}A$ which satisfy $q,$ can be carried out by a finite search.

Being in possession of complete algorithms for propositional calculus modeling, theorem checking, and theorem proving makes the analytic task fairly simple in principle, even if the question of efficiency in the face of arbitrary complexity remains another matter entirely.

The NP‑completeness of propositional satisfiability may weigh against the prospects of a single efficient algorithm capable of covering the whole space $[\mathrm{E}\mathcal{A}]$ with equal facility but there appears to be much room for improvement in classifying special forms and developing algorithms tailored to their practical processing.

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

Differential Propositional Calculus • 18

Posted on December 8, 2023 by Jon Awbrey

The Extended Universe of Discourse

The extended basis $\mathrm{E}\mathcal{A}$ of a universe of discourse $[\mathcal{A}]$ is formed by taking the initial basis $\mathcal{A}$ together with the differential basis $\mathrm{d}\mathcal{A}.$ Thus we have the following formula.

$\mathrm{E}\mathcal{A} ~=~ \mathcal{A} \cup \mathrm{d}\mathcal{A} ~=~ \{ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}.$

This supplies enough material to construct the differential extension $\mathrm{E}A$ of the space $A,$ also called the tangent bundle of $A,$ in the following fashion.

$\mathrm{E}A ~=~ \langle \mathrm{E}\mathcal{A} \rangle ~=~ \langle \mathcal{A} \cup \mathrm{d}\mathcal{A} \rangle ~=~ \langle a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle$

and also

$\mathrm{E}A ~=~ A \times \mathrm{d}A ~=~ A_1 \times \ldots \times A_n \times \mathrm{d}A_1 \times \ldots \times \mathrm{d}A_n.$

That gives $\mathrm{E}A$ the type $\mathbb{B}^n \times \mathbb{D}^n.$

Finally, the extended universe $\mathrm{E}A^\bullet = [\mathrm{E}\mathcal{A}]$ is the full collection of points and functions, or interpretations and propositions, based on the extended set of features $\mathrm{E}\mathcal{A},$ a fact summed up in the following notation.

$\mathrm{E}A^\bullet ~=~ [\mathrm{E}\mathcal{A}] ~=~ [a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n].$

That gives the extended universe $\mathrm{E}A^\bullet$ the following type.

$(\mathbb{B}^n \times \mathbb{D}^n\ +\!\to \mathbb{B}) ~=~ (\mathbb{B}^n \times \mathbb{D}^n, (\mathbb{B}^n \times \mathbb{D}^n \to \mathbb{B})).$

A proposition in the extended universe $[\mathrm{E}\mathcal{A}]$ is called a differential proposition and forms the logical analogue of a system of differential equations, constraints, or relations in ordinary calculus.

With these constructions, the differential extension $\mathrm{E}A$ and the space of differential propositions $(\mathrm{E}A \to \mathbb{B}),$ we arrive at the launchpad of our space explorations.

Table 11 summarizes the notations needed to describe the first order differential extensions of propositional calculi in a systematic manner.

$\text{Table 11. Differential Extension} \stackrel{_\bullet}{} \text{Basic Notation}$

The adjective differential or tangent is systematically attached to every construct based on the differential alphabet $\mathrm{d}\mathfrak{A},$ taken by itself. In like fashion, the adjective extended or the substantive bundle is systematically attached to any construct associated with the full complement of ${2n}$ features.

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

Differential Propositional Calculus • 17

Posted on December 6, 2023 by Jon Awbrey

Differential Propositions • Tangent Spaces

The tangent space to $A$ at one of its points $x,$ sometimes written $\mathrm{T}_x(A),$ takes the form $\mathrm{d}A$ $=$ $\langle \mathrm{d}\mathcal{A} \rangle$ $=$ $\langle \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle.$ Strictly speaking, the name cotangent space is probably more correct for this construction but since we take up spaces and their duals in pairs to form our universes of discourse it allows our language to be pliable here.

Proceeding as we did with the base space $A,$ the tangent space $\mathrm{d}A$ at a point of $A$ may be analyzed as the following product of distinct and independent factors.

$\mathrm{d}A ~=~ \displaystyle \prod_{i=1}^n \mathrm{d}A_i ~=~ \mathrm{d}A_1 \times \ldots \times \mathrm{d}A_n.$

Each factor $\mathrm{d}A_i$ is a set consisting of two differential propositions, $\mathrm{d}A_i = \{ (\mathrm{d}a_i), \mathrm{d}a_i \},$ where $\texttt{(} \mathrm{d}a_i \texttt{)}$ is a proposition with the logical value of $\lnot\mathrm{d}a_i.$ Each component $\mathrm{d}A_i$ has the type $\mathbb{B},$ operating under the ordered correspondence $\{ \texttt{(} \mathrm{d}a_i \texttt{)}, \mathrm{d}a_i \} \cong \{ 0, 1 \}.$ A measure of clarity is achieved, however, by acknowledging the differential usage with a superficially distinct type $\mathbb{D},$ whose sense may be indicated as follows.

$\mathbb{D} = \{ \texttt{(} \mathrm{d}a_i \texttt{)}, \mathrm{d}a_i \} = \{ \text{same}, \text{different} \} = \{ \text{stay}, \text{change} \} = \{ \text{stop}, \text{step} \}.$

Viewed within a coordinate representation, spaces of type $\mathbb{B}^n$ and $\mathbb{D}^n$ may appear to be identical sets of binary vectors, but taking a view at that level of abstraction would be like ignoring the qualitative units and the diverse dimensions that distinguish position and momentum, or the different roles of quantity and impulse.

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

Differential Propositional Calculus • 16

Posted on December 5, 2023 by Jon Awbrey

Differential Propositions • Qualitative Analogues of Differential Equations

The differential extension of a universe of discourse $[\mathcal{A}]$ is constructed by extending its initial alphabet $\mathfrak{A}$ to include a set of symbols for differential features, or basic changes capable of occurring in $[\mathcal{A}].$ The added symbols are taken to denote primitive features of change, qualitative attributes of motion, or propositions about how items in the universe of discourse may change or move in relation to features noted in the original alphabet.

With that in mind we define the corresponding differential alphabet or tangent alphabet $\mathrm{d}\mathfrak{A}$ $=$ $\{``\mathrm{d}a_1", \ldots, ``\mathrm{d}a_n"\},$ in principle just an arbitrary alphabet of symbols, disjoint from the initial alphabet $\mathfrak{A}$ $=$ $\{``a_1", \ldots, ``a_n"\}$ and given the meanings just indicated.

In practice the precise interpretation of the symbols in $\mathrm{d}\mathfrak{A}$ is conceived to be changeable from point to point of the underlying space $A.$ Indeed, for all we know, the state space $A$ might well be the state space of a language interpreter, one concerned with the idiomatic meanings of the dialect generated by $\mathfrak{A}$ and $\mathrm{d}\mathfrak{A}.$

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

Differential Propositional Calculus • 15

Posted on December 4, 2023 by Jon Awbrey

Fire over water:
The image of the condition before transition.
Thus the superior man is careful
In the differentiation of things,
So that each finds its place.

— I Ching ䷿ Hexagram 64

Differential Extension of Propositional Calculus

This much preparation is enough to begin introducing my subject, if I excuse myself from giving full arguments for my definitional choices until a later stage. To express the goal in a turn of phrase, the aim is to develop a differential theory of qualitative equations, one which can parallel the application of differential geometry to dynamical systems. The idea of a tangent vector is key to the work and a major goal is to find the right logical analogues of tangent spaces, bundles, and functors. The strategy is taken of looking for the simplest versions of those constructions which can be discovered within the realm of propositional calculus, so long as they serve to fill out the general theme.

Reference

Wilhelm, R., and Baynes, C.F. (trans.), The I Ching, or Book of Changes,
Foreword by C.G. Jung, Preface by H. Wilhelm, 3rd edition, Bollingen Series XIX, Princeton University Press, Princeton, NJ, 1967.

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

Differential Propositional Calculus • Discussion 7

Posted on December 2, 2023 by Jon Awbrey

Re: Differential Propositional Calculus • Discussion 1
Re: Reinaldo Cristo • Comment 1

RC:: We can say that emptiness came first, as it is the basis of the invention of mathematics, our perception, and numerical base 2. Do you agree or disagree?

A great many things in life and mathematics are built up through the persistent application of the most elementary steps to the humblest of beginnings.

So there may be something to that.

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Differential Propositional Calculus • 14

Posted on November 30, 2023 by Jon Awbrey

Differential Extensions

Table 11 summarizes the notations needed to describe the first order differential extensions of propositional calculi in a systematic manner.

$\text{Table 11. Differential Extension} \stackrel{_\bullet}{} \text{Basic Notation}$

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 4
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 3
	Survey of Differenti… on Differential Logic • 2
	Survey of Differenti… on Differential Logic • 1

Inquiry Into Inquiry

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Inquiry Driven Systems

Cybernetics

Differential Logic

Logical Graphs

Minimal Negation Operators

Peirce Matters

Relation Theory

Riffs & Rotes

Semeiotics

Theme One

Current Events

Fawkes News

Meta

A One-Dimensional Universe (cont.)

Resources

Share this:

A One‑Dimensional Universe

Resources

Share this:

Back to the Beginning • Exemplary Universes

Resources

Share this:

Life on Easy Street

Resources

Share this:

The Extended Universe of Discourse

Resources

Share this:

Differential Propositions • Tangent Spaces

Resources

Share this:

Differential Propositions • Qualitative Analogues of Differential Equations

Resources

Share this:

Differential Extension of Propositional Calculus

Reference

Resources

Share this:

Share this:

Differential Extensions

Resources

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta