Re: Drives and Their Vicissitudes • Fourth Gear Orbits
Re: Laws of Form • Lyle Anderson
- LA:
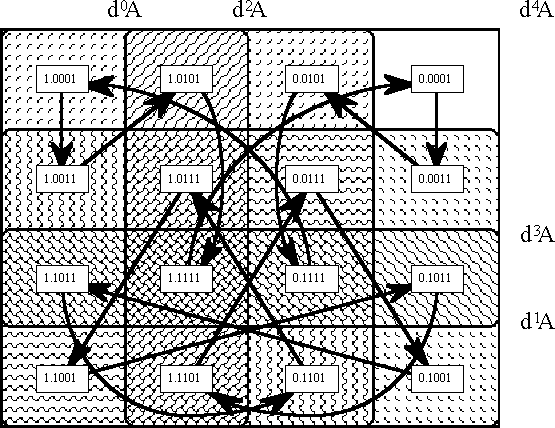
- Some of your diagrams, specifically Figure 16. A Couple of Fourth Gear Orbits, are beginning to look like Heim’s sketches for the structure of the photon. […] I can’t quite see the connection, yet, but maybe you can.
Lyle,
There is a curious analogy between the primitive operations which lie at the basis of logical graphs and basic themes of quantum mechanics, for example, the evaluation of a minimal negation operator proceeds in a manner reminiscent of the way a wave function collapses. That’s something I noticed early on in my work on logical graphs but I haven’t got much further than the mere notice so far.
I confess I’ve never gotten around to tackling Heim’s work — Peirce and Spencer Brown have loaded more than enough on my plate for any one lifetime — I do see lots of partial derivatives so maybe there’s a connection there — if I had to guess I would imagine any structure generated by a differential law as simple as what we have here is bound to find itself inhabiting all sorts of mathematical niches.
Regards,
Jon
Resources
cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science



![Tacit Extension of [A] to [A, dA]](https://inquiryintoinquiry.com/wp-content/uploads/2023/12/differential-logic-e280a2-tacit-extensions.png?w=640&h=240)
