Inquiry Into Inquiry

Transformations of Logical Graphs • 12

Posted on May 16, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (8) • (9) • (10) • (11)
Re: Interpretive Duality as Sign Relation • Orbit Order

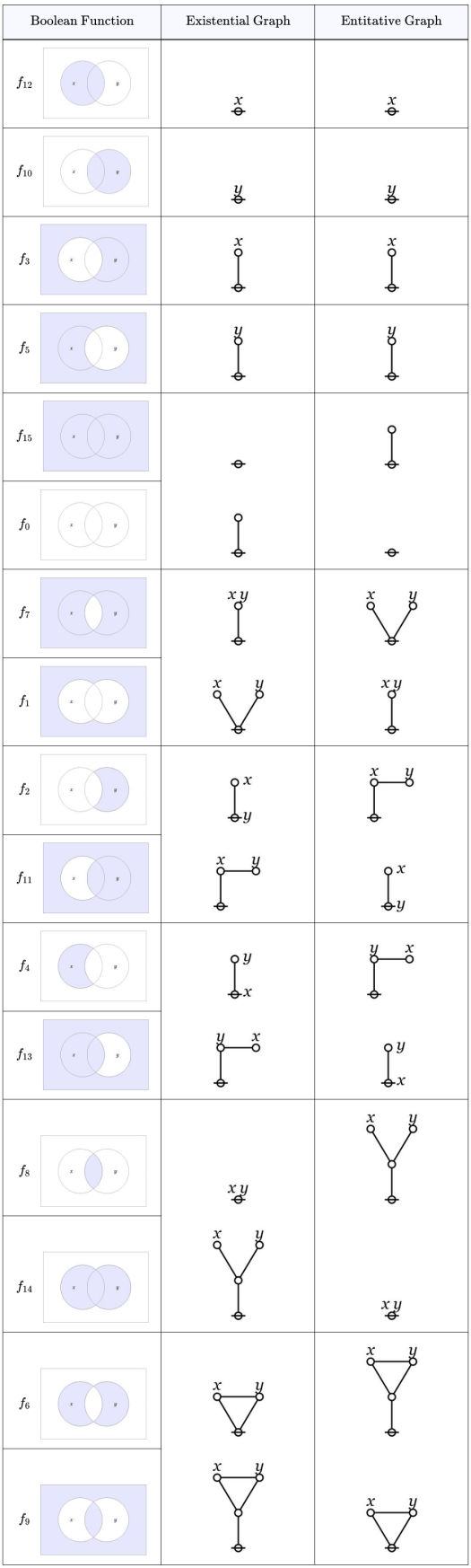
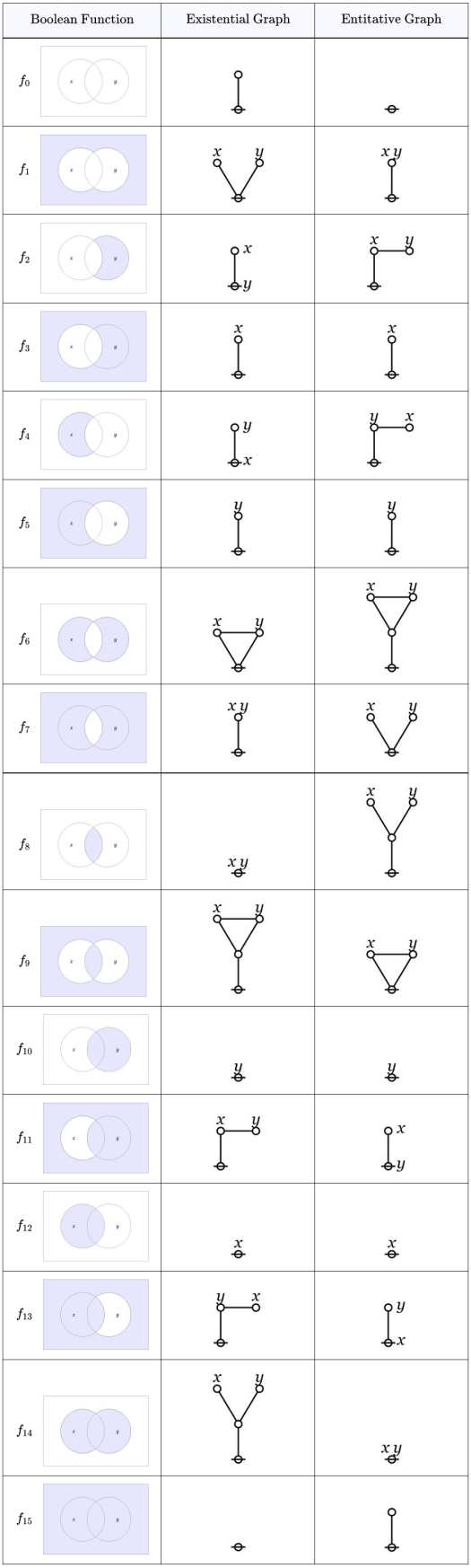
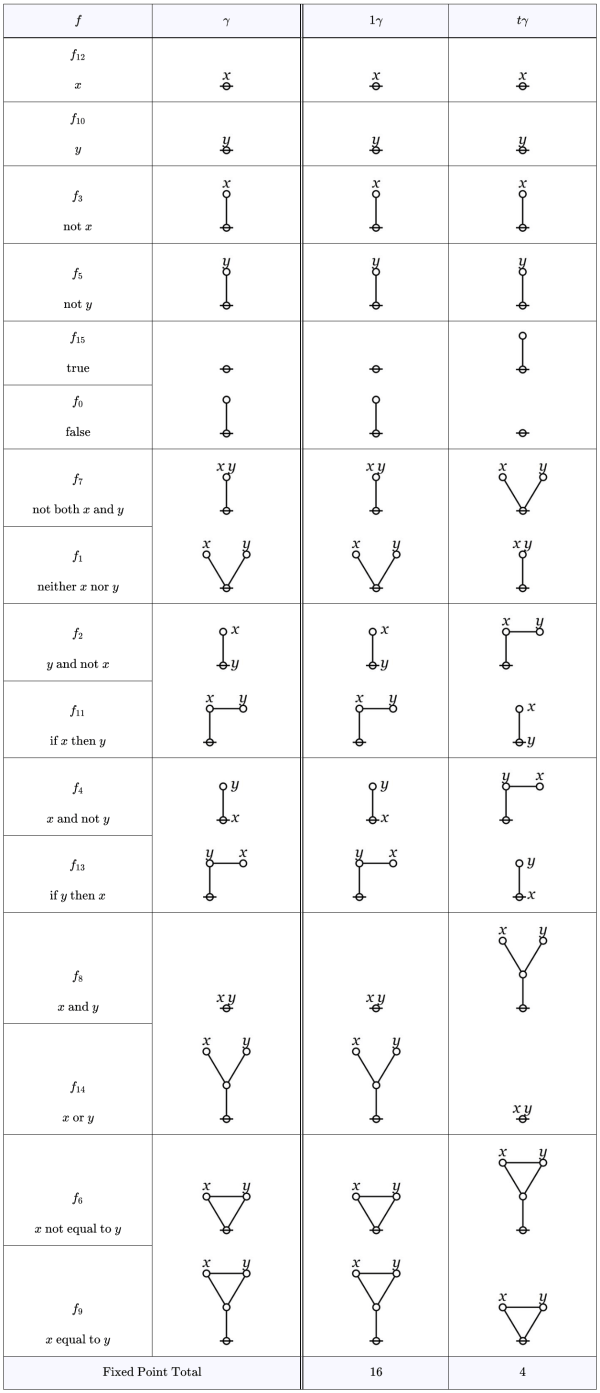
Taking from our wallets an old schedule of orbits, let’s review the classes of logical graphs we’ve covered so far.

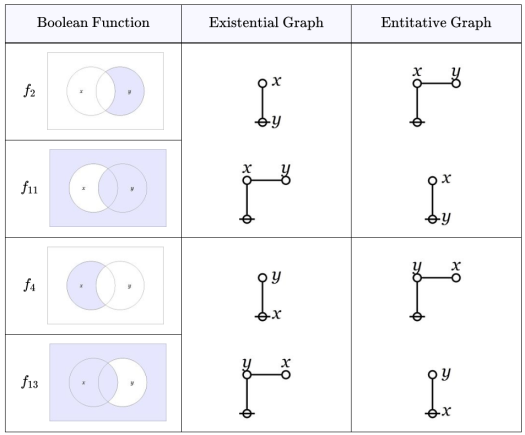
Self-Dual Logical Graphs

Four orbits of self‑dual logical graphs, $x, y, \texttt{(} x \texttt{)}, \texttt{(} y \texttt{)},$ were discussed in Episode 9.

The logical graphs $x, y, \texttt{(} x \texttt{)}, \texttt{(} y \texttt{)}$ denote the boolean functions $f_{12}, f_{10}, f_{3}, f_{5},$ in that order. The value of each function $f$ at each point $(x, y)$ in $\mathbb{B} \times \mathbb{B}$ is shown in the Table above.

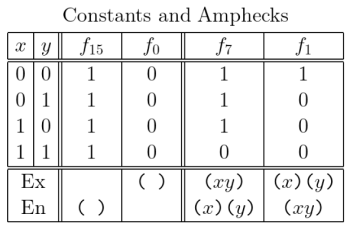
Constants and Amphecks

Two orbits of logical graphs called constants and amphecks were discussed in Episode 10.

The constant logical graphs denote the constant functions

$f_{0} : \mathbb{B} \times \mathbb{B} \to 0 \quad \text{and} \quad f_{15} : \mathbb{B} \times \mathbb{B} \to 1.$

Under $\mathrm{Ex}$ the logical graph whose text form is “ ” denotes the function $f_{15}$
and the logical graph whose text form is $``\texttt{(} ~ \texttt{)}"$ denotes the function $f_{0}.$
Under $\mathrm{En}$ the logical graph whose text form is “ ” denotes the function $f_{0}$
and the logical graph whose text form is $``\texttt{(} ~ \texttt{)}"$ denotes the function $f_{15}.$

The ampheck logical graphs denote the ampheck functions

$f_{1}(x, y) = \textsc{nnor}(x, y) \quad \text{and} \quad f_{7}(x, y) = \textsc{nand}(x, y).$

Under $\mathrm{Ex}$ the logical graph $\texttt{(} xy \texttt{)}$ denotes the function $f_{7}(x, y) = \textsc{nand}(x, y)$
and the logical graph $\texttt{(} x \texttt{)(} y \texttt{)}$ denotes the function $f_{1}(x, y) = \textsc{nnor}(x, y).$
Under $\mathrm{En}$ the logical graph $\texttt{(} xy \texttt{)}$ denotes the function $f_{1}(x, y) = \textsc{nnor}(x, y)$
and the logical graph $\texttt{(} x \texttt{)(} y \texttt{)}$ denotes the function $f_{7}(x, y) = \textsc{nand}(x, y).$

Subtractions and Implications

The logical graphs called subtractions and implications were discussed in Episode 11.

The subtraction logical graphs denote the subtraction functions

$f_{2}(x, y) = y \lnot x \quad \text{and} \quad f_{4}(x, y) = x \lnot y.$

The implication logical graphs denote the implication functions

$f_{11}(x, y) = x \Rightarrow y \quad \text{and} \quad f_{13}(x, y) = y \Rightarrow x.$

Under the action of the $\mathrm{En} \leftrightarrow \mathrm{Ex}$ duality the logical graphs for the subtraction $f_{2}$ and the implication $f_{11}$ fall into one orbit while the logical graphs for the subtraction $f_{4}$ and the implication $f_{13}$ fall into another orbit, making these two partitions of the four functions orthogonal or transversal to each other.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Interpretive Duality, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Interpretive Duality, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Visualization | 4 Comments

Transformations of Logical Graphs • 11

Posted on May 15, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (8) • (9) • (10)

Continuing our scan of the Table in Episode 8, the next two orbits contain the logical graphs for the boolean functions $f_{2}, f_{11}, f_{4}, f_{13},$ in that order. A first glance shows the two orbits have surprisingly intricate structures and relationships to each other — let’s isolate that section for a closer look.

$\text{Interpretive Duality} \stackrel{_\bullet}{} \text{Subtractions and Implications}$

The boolean functions $f_{2}$ and $f_{4}$ are called subtraction functions.
The boolean functions $f_{11}$ and $f_{13}$ are called implication functions.

The logical graphs for $f_{2}$ and $f_{11}$ are dual to each other.
The logical graphs for $f_{4}$ and $f_{13}$ are dual to each other.

The values of the subtraction and implication functions for each $(x, y) \in \mathbb{B} \times \mathbb{B}$ and the text expressions for their logical graphs are given in the following Table.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 10

Posted on May 14, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6) • (7) • (8) • (9)

After the four orbits of self‑dual logical graphs we come to six orbits of dual pairs. In no particular order of importance, we may start by considering the following two.

The logical graphs for the constant functions $f_{15}$ and $f_{0}$ are dual to each other.
The logical graphs for the ampheck functions $f_{7}$ and $f_{1}$ are dual to each other.

The values of the constant and ampheck functions for each $(x, y) \in \mathbb{B} \times \mathbb{B}$ and the text expressions for their logical graphs are given in the following Table.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 9

Posted on May 13, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6) • (7) • (8)

Last time we took up the four singleton orbits in the action of $T$ on $X$ and saw each consists of a single logical graph which $T$ fixes, preserves, or transforms into itself. On that account those four logical graphs are said to be self‑dual or $T$ ‑invariant.

In general terms, it is useful to think of the entitative and existential interpretations as two formal languages which happen to use the same set of signs, each in its own way, to denote the same set of formal objects. Then $T$ defines the translation between languages and the self‑dual logical graphs are the points where the languages coincide, where the same signs denote the same objects in both. Such constellations of “fixed stars” are indispensable to navigation between languages, as every argot‑naut discovers in time.

Returning to the case at hand, where $T$ acts on a selection of 16 logical graphs for the 16 boolean functions on two variables, the following Table shows the values of the denoted boolean function $f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}$ for each of the self‑dual logical graphs.

The functions indexed here as $f_{12}$ and $f_{10}$ are known as the coordinate projections $(x, y) \mapsto x$ and $(x, y) \mapsto y$ on the first and second coordinates, respectively, and the functions indexed as $f_{3}$ and $f_{5}$ are the negations $(x, y) \mapsto \tilde{x}$ and $(x, y) \mapsto \tilde{y}$ of those projections, respectively.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 8

Posted on May 12, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6) • (7)

Turning again to our Table of Orbits let’s see what we can learn about the structure of the sign relational system in view.

As we saw in Episode 2, the transformation group $T = \{ 1, t \}$ partitions the set $X$ of 16 logical graphs and also the set $O$ of 16 boolean functions into 10 orbits, all together amounting to 4 singleton orbits and 6 doubleton orbits.

Points in singleton orbits are called fixed points of the transformation group $T : X \to X$ since they are left unchanged, or changed into themselves, by all group actions. Viewed in the frame of the sign relation $L \subseteq O \times X \times X,$ where the transformations in $T$ are literally translations in the linguistic sense, these $T$ -invariant graphs have the same denotations in $O$ for both Existential Interpreters and Entitative Interpreters.

$\text{Interpretive Duality as Sign Relation} \stackrel{_\bullet}{} \text{Orbit Order}$

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 7

Posted on May 11, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6)

Our investigation has brought us to the point of seeing both a transformation group and a triadic sign relation in the duality between entitative and existential interpretations of logical graphs.

Given the level of the foregoing abstractions it helps to anchor them in concrete structural experience. In that spirit we’ve been pursuing the case of a group action $T : X \to X$ and a sign relation $L \subseteq O \times X \times X$ where $O$ is the set of boolean functions on two variables and $X$ is a set of logical graphs denoting those functions. We drew up a Table combining the aspects of both structures and sorted it according to the orbits $T$ induces on $X$ and consequently on $O.$

$\text{Interpretive Duality as Sign Relation} \stackrel{_\bullet}{} \text{Orbit Order}$

In the next few posts we’ll take up the orbits of logical graphs one by one, comparing and contrasting their syntax and semantics.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 6

Posted on May 10, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5)

Our study of the duality between entitative and existential interpretations of logical graphs has brought to light its fully sign-relational character, casting the interpretive duality as a transformation of signs revolving about a common object domain. The overall picture is a triadic relation linking an object domain with two sign domains, whose signs denote the objects in two distinct ways.

By way of constructing a concrete example, we let our object domain consist of the 16 boolean functions on 2 variables and we let our sign domains consist of representative logical graphs for those 16 functions. Thus we arrived at the Table in the previous post, linked by its title below.

$\text{Interpretive Duality as Sign Relation}$

Column 1 shows the object domain $O$ as the set of 16 boolean functions on 2 variables.
Column 2 shows the sign domain $S$ as a representative set of logical graphs denoting the objects in $O$ according to the existential interpretation.
Column 3 shows the interpretant domain $I$ as the same set of logical graphs denoting the objects in $O$ according to the entitative interpretation.

Additional aspects of the sign relation’s structure can be brought out by sorting the Table in accord with the orbits induced on the object domain by the group action inherent in the interpretive duality. Performing that sort produces the following Table.

$\text{Interpretive Duality as Sign Relation} \stackrel{_\bullet}{} \text{Orbit Order}$

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 5

Posted on May 9, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4)

“I know what you mean but I say it another way” — it’s a thing I find myself saying often enough, if only under my breath, to rate an acronym for it ☞ IKWYMBISIAW ☜ and not too coincidentally it’s a rubric of relevance to many situations in semiotics where sundry manners of speaking and thinking converge, more or less, on the same patch of pragmata.

We encountered just such a situation in our exploration of the duality between entitative and existential interpretations of logical graphs. The two interpretations afford distinct but equally adequate ways of reasoning about a shared objective domain. To cut our teeth on a simple but substantial example of an object domain, we picked the space of boolean functions or propositional forms on two variables. That brought us to the following Table, highlighting the sign relation $L \subseteq O \times S \times I$ involved in switching between existential and entitative interpretations of logical graphs.

$\text{Interpretive Duality as Sign Relation}$

Column 1 shows the object domain $O$ as the set of 16 boolean functions on 2 variables.
Column 2 shows the sign domain $S$ as a representative set of logical graphs denoting the objects in $O$ according to the existential interpretation.
Column 3 shows the interpretant domain $I$ as the same set of logical graphs denoting the objects in $O$ according to the entitative interpretation.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 4

Posted on May 8, 2024 by Jon Awbrey

Semiotic Transformations

Once we bring the dual interpretations of logical graphs to the same Table and relate their parleys to the same objects, it is clear we are dealing with a triadic sign relation of the sort taken up in C.S. Peirce’s semiotics or theory of signs.

A sign relation $L \subseteq O \times S \times I,$ as a set $L$ embedded in a cartesian product $O \times S \times I,$ tells how the signs in $S$ and the interpretant signs in $I$ correlate with the objects or objective situations in $O.$

There are many ways of using sign relations to model various types of sign‑theoretic situations and processes. The following cases are often seen.

Some sign relations model co‑referring signs or transitions between signs within a single language or symbol system. In that event $L \subseteq O \times S \times I$ has $S = I.$
Other sign relations model translations between different languages or different interpretations of the same language, in other words, different ways of referring the same set of signs to a shared object domain.

The next Table extracts the sign relation $L \subseteq O \times S \times I$ involved in switching between existential and entitative interpretations of logical graphs.

Column 1 shows the object domain $O$ as the set of 16 boolean functions on 2 variables.
Column 2 shows the sign domain $S$ as a representative set of logical graphs denoting the objects in $O$ according to the existential interpretation.
Column 3 shows the interpretant domain $I$ as the same set of logical graphs denoting the objects in $O$ according to the entitative interpretation.

$\text{Interpretive Duality as Sign Relation}$

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 3

Posted on May 7, 2024 by Jon Awbrey

Re: Transformations of Logical Graphs • (1) • (2)

We’ve been using the duality between entitative and existential interpretations of logical graphs to get a handle on the mathematical forms pervading logical laws. A few posts ago we took up the tools of groups and symmetries and transformations to study the duality and we looked to the space of 2-variable boolean functions as a basic training grounds. On those grounds the translation between interpretations presents as a group $G$ of order two acting on a set $X$ of sixteen logical graphs denoting boolean functions.

Last time we arrived at a Table showing how the group $G$ partitions the set $X$ into ten orbits of logical graphs. Here again is that Table.

$\text{Interpretive Duality as Group Symmetry} \stackrel{_\bullet}{} \text{Orbit Order}$

I invited the reader to investigate the relationship between the group order $|G| = 2,$ the number of orbits $10,$ and the total number of fixed points $16 + 4 = 20.$ In the present case the product of the group order (2) and the number of orbits (10) is equal to the sum of the fixed points (20) — Is that just a fluke? If not, why so? And does it reflect a general rule?

We can make a beginning toward answering those questions by inspecting the incidence relation of fixed points and orbits in the Table above. Each singleton orbit accumulates two hits, one from the group identity and one from the other group operation. But each doubleton orbit also accumulates two hits, since the group identity fixes both of its two points. Thus all the orbits are double-counted by counting the incidence of fixed points and orbits. In sum, dividing the total number of fixed points by the order of the group brings us back to the exact number of orbits.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

	Survey of Differenti… on Differential Logic • 4
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 3
	Survey of Differenti… on Differential Logic • 2
	Survey of Differenti… on Differential Logic • 1
	Survey of Differenti… on Differential Logic • Over…
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…

M	T	W	T	F	S	S
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28

Semiotic Transformations

Self-Dual Logical Graphs

Constants and Amphecks

Subtractions and Implications

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Resources

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta