I would really like to have slipped imperceptibly into this lecture, as into all the others I shall be delivering, perhaps over the years ahead.
— Michel Foucault • The Discourse on Language
Tacit Extensions
In viewing the previous Table of Differential Propositions it is important to notice the subtle distinction in type between a function  and its inclusion as a function
and its inclusion as a function  even though they share the same logical expression. Naturally, we want to maintain the logical equivalence of expressions representing the same proposition while appreciating the full diversity of a proposition’s functional and typical representatives. Both perspectives, and all the levels of abstraction extending through them, have their reasons, as will develop in time.
even though they share the same logical expression. Naturally, we want to maintain the logical equivalence of expressions representing the same proposition while appreciating the full diversity of a proposition’s functional and typical representatives. Both perspectives, and all the levels of abstraction extending through them, have their reasons, as will develop in time.
Because this special circumstance points to a broader theme, it’s a good idea to discuss it more generally. Whenever there arises a situation like that above, where one basis  is a subset of another basis
is a subset of another basis  we say any proposition
we say any proposition  has a tacit extension to a proposition
has a tacit extension to a proposition  and we say the space
and we say the space  has an automatic embedding within the space
has an automatic embedding within the space 
The tacit extension operator  is defined in such a way that
is defined in such a way that  puts the same constraint on the variables of
puts the same constraint on the variables of  within
within  as the proposition
as the proposition  initially put on
initially put on  while it puts no constraint on the variables of
while it puts no constraint on the variables of  beyond
beyond  in effect, conjoining the two constraints.
in effect, conjoining the two constraints.
Indexing the variables as  and
and  the tacit extension from
the tacit extension from  to
to  may be expressed by the following equation.
may be expressed by the following equation.

On formal occasions, such as the present context of definition, the tacit extension from  to
to  is explicitly symbolized by the operator
is explicitly symbolized by the operator  where the bases
where the bases  and
and  are set in context, but it’s normally understood the
are set in context, but it’s normally understood the  may be silent.
may be silent.
Resources
cc: Academia.edu • Cybernetics • Structural Modeling • Systems Science
cc: Conceptual Graphs • Laws of Form • Mathstodon • Research Gate
are shown in the next two Figures.




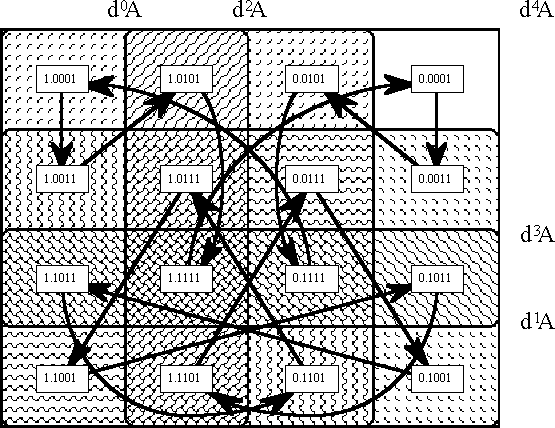
![Tacit Extension of [A] to [A, dA]](https://inquiryintoinquiry.com/wp-content/uploads/2023/12/differential-logic-e280a2-tacit-extensions.png?w=640&h=240)
