Differential Logic • 17

Posted on November 22, 2024 by Jon Awbrey

Enlargement and Difference Maps

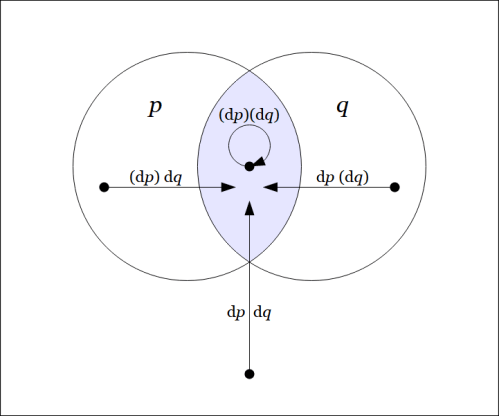
Continuing with the example pq : X \to \mathbb{B}, the following venn diagram shows the enlargement or shift map \mathrm{E}(pq) : \mathrm{E}X \to \mathbb{B} in the same style of field picture we drew for the tacit extension \boldsymbol\varepsilon (pq) : \mathrm{E}X \to \mathbb{B}.

Enlargement E(pq) : EX → B
\text{Enlargement}~ \mathrm{E}(pq) : \mathrm{E}X \to \mathbb{B}

\begin{array}{rcccccc} \mathrm{E}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{(} \mathrm{d}p \texttt{)~} \mathrm{d}q \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \mathrm{d}p \texttt{~(} \mathrm{d}q \texttt{)} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \mathrm{d}p \texttt{~~} \mathrm{d}q \texttt{~} \end{array}

A very important conceptual transition has just occurred here, almost tacitly, as it were.  Generally speaking, having a set of mathematical objects of compatible types, in this case the two differential fields \boldsymbol\varepsilon f and \mathrm{E}f, both of the type \mathrm{E}X \to \mathbb{B}, is very useful, because it allows us to consider those fields as integral mathematical objects which can be operated on and combined in the ways we usually associate with algebras.

In the present case one notices the tacit extension \boldsymbol\varepsilon f and the enlargement \mathrm{E}f are in a sense dual to each other.  The tacit extension \boldsymbol\varepsilon f indicates all the arrows out of the region where f is true and the enlargement \mathrm{E}f indicates all the arrows into the region where f is true.  The only arc they have in common is the no‑change loop \texttt{(} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{)} at pq.  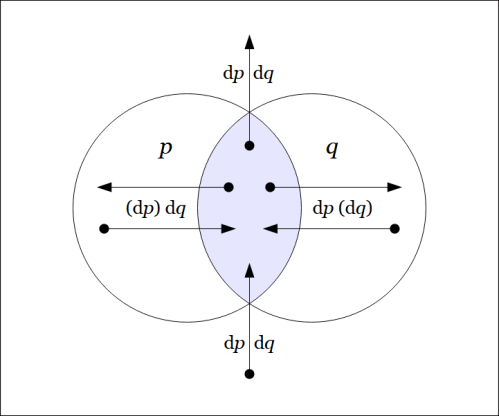If we add the two sets of arcs in mod 2 fashion then the loop of multiplicity 2 zeroes out, leaving the 6 arrows of \mathrm{D}(pq) = \boldsymbol\varepsilon(pq) + \mathrm{E}(pq) shown in the following venn diagram.

Differential D(pq) : EX → B
\text{Difference}~ \mathrm{D}(pq) : \mathrm{E}X \to \mathbb{B}

\begin{array}{rcccccc} \mathrm{D}(pq) & = & p & \cdot & q & \cdot & \texttt{((} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{))} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~(} \mathrm{d}p \texttt{)~} \mathrm{d}q \texttt{~~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~~} \mathrm{d}p \texttt{~(} \mathrm{d}q \texttt{)~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(}q \texttt{)} & \cdot & \texttt{~~} \mathrm{d}p \texttt{~~} \mathrm{d}q \texttt{~~} \end{array}

Resources

cc: Academia.edu • Cybernetics • Structural Modeling • Systems Science
cc: Conceptual Graphs • Laws of Form • Mathstodon • Research Gate

This entry was posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Change, Cybernetics, Differential Calculus, Differential Logic, Discrete Dynamics, Equational Inference, Functional Logic, Gradient Descent, Graph Theory, Inquiry Driven Systems, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Propositional Calculus, Time, Zeroth Order Logic and tagged , , , , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.

4 Responses to Differential Logic • 17

  1. Pingback: Survey of Differential Logic • 7 | Inquiry Into Inquiry

  2. Pingback: Survey of Differential Logic • 7 | Inquiry Into Inquiry

  3. Pingback: Survey of Differential Logic • 8 | Inquiry Into Inquiry

  4. Pingback: Survey of Differential Logic • 8 | Systems Community of Inquiry

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.