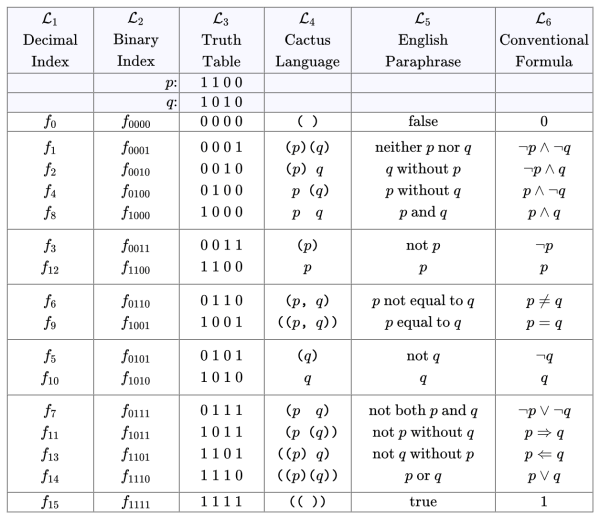
Propositional Forms on Two Variables

Tables A1 and A2 showed two ways of organizing the sixteen boolean functions or propositional forms on two variables, as expressed in several notations.  In future discussions the two Tables will be described as the Index Order and the Orbit Order of propositions, respectively, “orbits” being the usual term in mathematics for similarity classes under a group action.  For ease of comparison, here are fresh copies of both Tables on the same page.

Recalling the discussion up to this point, we took as our first example the boolean function corresponding to the logical conjunction and examined how the differential operators and act on   Each operator takes the boolean function of two variables and gives back a boolean function of four variables, and respectively.

In the next several posts we’ll extend our scope to the full set of boolean functions on two variables and examine how the differential operators and act on that set.  There being some advantage to singling out the enlargement or shift operator in its own right, we’ll begin by computing for each function in the above Tables.

Resources

• Logic Syllabus
• Survey of Differential Logic

cc: Academia.edu • Cybernetics • Structural Modeling • Systems Science
cc: Conceptual Graphs • Laws of Form • Ma^thstodon • Research Gate