And if he is told that something is the way it is, then he thinks:  Well, it could probably just as easily be some other way.  So the sense of possibility might be defined outright as the capacity to think how everything could “just as easily” be, and to attach no more importance to what is than to what is not.

— Robert Musil • The Man Without Qualities

To get a clearer view of the relation between primary arithmetic and primary algebra consider the following extremely simple algebraic expression.

Here we see the variable name appearing as an operand name in the expression   In functional terms, is called an argument name but it’s best to avoid the potentially confusing connotations of the word argument here, since it also refers in logical discussions to a more or less specific pattern of reasoning.

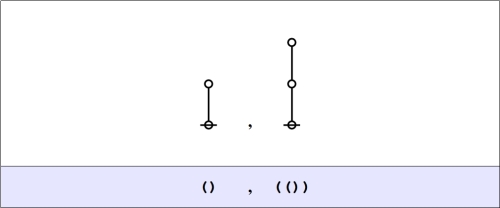
In effect, the algebraic variable name indicates the contemplated absence or presence of any arithmetic expression taking its place in the surrounding template, which expression is proxied well enough by its formal value, and of which values we know but two.  Putting it all together, the algebraic expression varies between the following two choices.

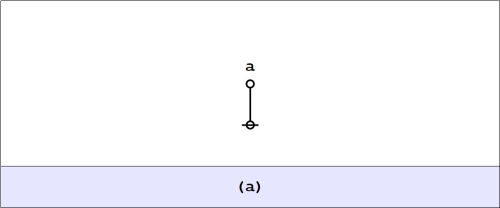
The above set of arithmetic expressions is what it means to contemplate the absence or presence of the arithmetic constant in the place of the operand in the algebraic expression   But what would it mean to contemplate the absence or presence of the operator in the algebraic expression

That is the question I’ll take up next.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science