Differential Propositional Calculus • 18

Posted on December 8, 2023 by Jon Awbrey

The Extended Universe of Discourse

The extended basis \mathrm{E}\mathcal{A} of a universe of discourse [\mathcal{A}] is formed by taking the initial basis \mathcal{A} together with the differential basis \mathrm{d}\mathcal{A}.  Thus we have the following formula.

\mathrm{E}\mathcal{A} ~=~ \mathcal{A} \cup \mathrm{d}\mathcal{A} ~=~ \{ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}.

This supplies enough material to construct the differential extension \mathrm{E}A of the space A, also called the tangent bundle of A, in the following fashion.

\mathrm{E}A ~=~ \langle \mathrm{E}\mathcal{A} \rangle ~=~ \langle \mathcal{A} \cup \mathrm{d}\mathcal{A} \rangle ~=~ \langle a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle

and also

\mathrm{E}A ~=~ A \times \mathrm{d}A ~=~ A_1 \times \ldots \times A_n \times \mathrm{d}A_1 \times \ldots \times \mathrm{d}A_n.

That gives \mathrm{E}A the type \mathbb{B}^n \times \mathbb{D}^n.

Finally, the extended universe \mathrm{E}A^\bullet = [\mathrm{E}\mathcal{A}] is the full collection of points and functions, or interpretations and propositions, based on the extended set of features \mathrm{E}\mathcal{A}, a fact summed up in the following notation.

\mathrm{E}A^\bullet ~=~ [\mathrm{E}\mathcal{A}] ~=~ [a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n].

That gives the extended universe \mathrm{E}A^\bullet the following type.

(\mathbb{B}^n \times \mathbb{D}^n\ +\!\to \mathbb{B}) ~=~ (\mathbb{B}^n \times \mathbb{D}^n, (\mathbb{B}^n \times \mathbb{D}^n \to \mathbb{B})).

A proposition in the extended universe [\mathrm{E}\mathcal{A}] is called a differential proposition and forms the logical analogue of a system of differential equations, constraints, or relations in ordinary calculus.

With these constructions, the differential extension \mathrm{E}A and the space of differential propositions (\mathrm{E}A \to \mathbb{B}), we arrive at the launchpad of our space explorations.

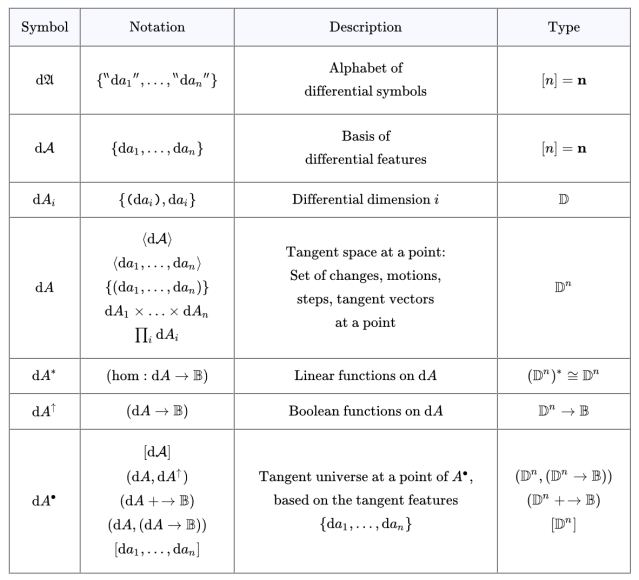
Table 11 summarizes the notations needed to describe the first order differential extensions of propositional calculi in a systematic manner.

\text{Table 11. Differential Extension} \stackrel{_\bullet}{} \text{Basic Notation}
Differential Extension • Basic Notation

The adjective differential or tangent is systematically attached to every construct based on the differential alphabet \mathrm{d}\mathfrak{A}, taken by itself.  In like fashion, the adjective extended or the substantive bundle is systematically attached to any construct associated with the full complement of {2n} features.

Resources

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs (1) (2) • Cybernetics • Structural Modeling • Systems Science

This entry was posted in Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Change, Computational Complexity, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamics, Dynamical Systems, Equational Inference, Functional Logic, Gradient Descent, Graph Theory, Group Theory, Hologrammautomaton, Indicator Functions, Logic, Logical Graphs, Mathematical Models, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Time, Visualization and tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.

2 Responses to Differential Propositional Calculus • 18

  1. Pingback: Survey of Differential Logic • 6 | Inquiry Into Inquiry

  2. Pingback: Survey of Differential Logic • 7 | Inquiry Into Inquiry

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.