Here are two ways of looking at the divisibility relation, a dyadic relation of fundamental importance in number theory.

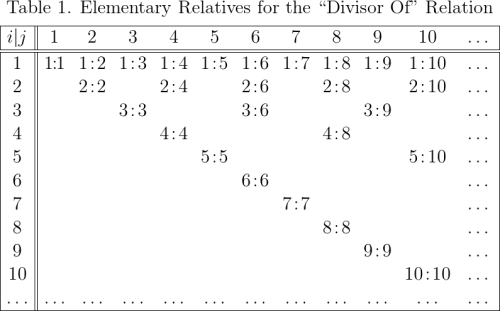
Table 1 shows the first few ordered pairs of the relation on positive integers corresponding to the relative term, “divisor of”.  Thus, the ordered pair appears in the relation if and only if divides for which the usual notation is

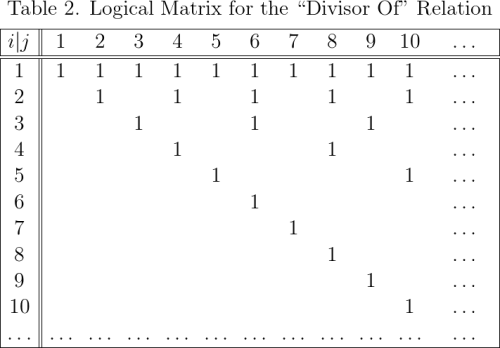
Table 2 shows the same information in the form of a logical matrix.  This has a coefficient of  in row and column when otherwise it has a coefficient of   (The zero entries have been omitted for ease of reading.)

Just as matrices in linear algebra represent linear transformations, these logical arrays and matrices represent logical transformations.

Resources

• Relation Theory
• Triadic Relations
• Sign Relations
• Peirce’s 1870 Logic Of Relatives

cc: Category Theory • Cybernetics • Ontolog • Structural Modeling • Systems Science
cc: FB | Relation Theory • Laws of Form • Peirce List