Frankl, My Dear • 7

Posted on October 29, 2014 by Jon Awbrey

Re: Dick Lipton & Ken Regan • (1) • (2)

We continue with the differential analysis of the proposition in Example 1.

Example 1


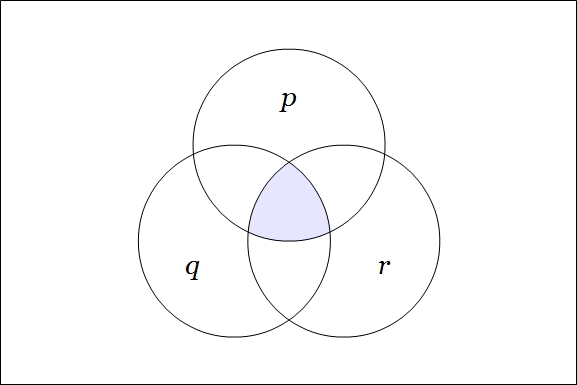Venn Diagram PQR		 (1)

A proposition defined on one universe of discourse has natural extensions to larger universes of discourse. As a matter of course in a given context of discussion, some of these extensions come to be taken for granted as the most natural extensions to make in passing from one universe to the next and they tend to be assumed automatically, by default, in the absence of explicit notice to the contrary. These are the tacit extensions that apply in that context.

Differential logic, at the first order of analysis, treats extensions from boolean spaces of type \mathbb{B}^k to enlarged boolean spaces of type \mathbb{B}^k \times \mathbb{D}^k. In this setting \mathbb{B} \cong \mathbb{D} \cong \{ 0, 1 \} but we use different letters merely to distinguish base and differential features.

In our present example, the tacit extension \boldsymbol\varepsilon f of f is the boolean function \boldsymbol\varepsilon f : \mathbb{B}^3 \times \mathbb{D}^3 \to \mathbb{B} defined by the following equation:

\boldsymbol\varepsilon f(p, q, r, \mathrm{d}p, \mathrm{d}q, \mathrm{d}r) ~=~ f(p, q, r).

The boolean expansion of \boldsymbol\varepsilon f takes the following form:

\boldsymbol\varepsilon f(p, q, r, \mathrm{d}p, \mathrm{d}q, \mathrm{d}r) =

\begin{array}{*{8}{l}} & p q r ~ \texttt{(} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{)(} \mathrm{d}r \texttt{)} & + & p q r ~ \texttt{(} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{)~} \mathrm{d}r \texttt{~} & + & p q r ~ \texttt{(} \mathrm{d}p \texttt{)~} \mathrm{d}q \texttt{~(} \mathrm{d}r \texttt{)} & + & p q r ~ \texttt{(} \mathrm{d}p \texttt{)~} \mathrm{d}q \texttt{~~} \mathrm{d}r \texttt{~} \\[4pt] + & p q r ~ \texttt{~} \mathrm{d}p \texttt{~(} \mathrm{d}q \texttt{)(} \mathrm{d}r \texttt{)} & + & p q r ~ \texttt{~} \mathrm{d}p \texttt{~(} \mathrm{d}q \texttt{)~} \mathrm{d}r \texttt{~} & + & p q r ~ \texttt{~} \mathrm{d}p \texttt{~~} \mathrm{d}q \texttt{~(} \mathrm{d}r \texttt{)} & + & p q r ~ \texttt{~} \mathrm{d}p \texttt{~~} \mathrm{d}q \texttt{~~} \mathrm{d}r \texttt{~} \end{array}

In other words, \boldsymbol\varepsilon f is simply f on the base variables p, q, r extended by a tautology — commonly known as a “Don’t Care” condition — on the differential variables \mathrm{d}p, \mathrm{d}q, \mathrm{d}r.

To be continued …

Resources

This entry was posted in Boolean Algebra, Boolean Functions, Computational Complexity, Differential Logic, Frankl Conjecture, Logic, Logical Graphs, Mathematics, Péter Frankl and tagged , , , , , , , , . Bookmark the permalink.