Inquiry Into Inquiry

Re: Cybernetics • Cliff Joslyn (1) (2) (3) (4)

Dear Cliff,

A few examples of sign relations and triadic relations may serve to illustrate the problem of their demarcation.

First, to clear up one point of notation, in writing there is no assumption on my part the relational domains are necessarily disjoint.  They may intersect or even be identical, as   Of course we rarely need to contemplate limiting cases of that type but I find it useful to keep them in our categorical catalogue.  (Other writers will differ on that score.)  On the other hand, we very often consider cases where as in the following two examples of sign relations discussed in Sign Relations • Examples.

We have the following data.

As I mentioned, those examples were deliberately constructed to be as simple as possible but they do exemplify many typical features of sign relations in general.  Until the time my advisor asked me for cases of that order I had always contemplated formal languages with countable numbers of signs and never really thought about finite sign relations at all.

Reference

• Charles S. Peirce (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.

Sources

• C.S. Peirce • On the Definition of Logic
• C.S. Peirce • Logic as Semiotic
• C.S. Peirce • Objective Logic

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

Re: Cybernetics • Cliff Joslyn (1) (2) (3)

Dear Cliff,

Backing up a little —

Whether a thing qualifies as a sign is not an ontological question, a matter of what it is in itself, but a pragmatic question, a matter of what role it plays in a particular application.

By extension, whether a triadic relation qualifies as a sign relation is not just a question of its abstract structure but a question of its potential applications, of its fitness for a particular purpose, namely, whether we can imagine it capturing aspects of objective structure immanent in the conduct of logical reasoning.

Because it’s difficult, and not even desirable, to place prior limits on “what we can imagine finding a use for”, there is seldom a good case for trying to reduce pragmatic definitions to ontological definitions.  That’s why I feel bound to leave the boundaries a bit fuzzy.

Just to sum up what I’ve been struggling to say here —

It’s not a bad idea to cast an oversized net at the outset, and the à priori method can take us a way with that, but developing semiotics beyond its first principles and early stages will depend on gathering more significant examples of sign relations and sign transformations approaching the level we actually employ in the practice of communication, computation, inquiry, learning, proof, and reasoning in general.  I think that’s probably the best way to see the real sense and utility of Peirce’s double definition of logic and signs.

Reference

• Charles S. Peirce (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.

Sources

• C.S. Peirce • On the Definition of Logic
• C.S. Peirce • Logic as Semiotic
• C.S. Peirce • Objective Logic

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

Re: Cybernetics • Cliff Joslyn

CJ:

For a given arbitrary triadic relation (let’s say that 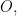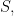and are all finite, non‑empty sets), I’m interested to understand what additional axioms you’re saying are necessary and sufficient to make a sign relation.  I checked Sign Relations • Definition, but it wasn’t obvious, or at least, not formalized.

Dear Cliff,

From a purely speculative point of view, any triadic relation on any set might be capable of capturing aspects of objective structure immanent in the conduct of logical reasoning.  At least I can think of no reason to exclude the possibility à priori.

When we turn to the task of developing computational adjuncts to inquiry there is still no harm in keeping arbitrary triadic relations in mind, as entire hosts of them will turn up on the universe side of many universes of discourse we happen to encounter, if nowhere else.

Peirce’s use of the word definition understandably leads us to anticipate a strictly apodictic development, say, along the lines of abstract group theory or axiomatic geometry.  In that light I often look to group theory for hints on how to go about tackling a category of triadic relations such as we find in semiotics.  The comparison makes for a very rough guide but the contrasts are also instructive.

More than that, the history of group theory, springing as it did as yet unnamed from the ground of pressing mathematical problems, from Newton’s use of symmetric functions and Galois’ application of permutation groups to the theory of equations among other sources, tells us what state of development we might reasonably expect from the current still early days of semiotics.

To be continued …

Reference

• Charles S. Peirce (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.

Sources

• C.S. Peirce • On the Definition of Logic
• C.S. Peirce • Logic as Semiotic
• C.S. Peirce • Objective Logic

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

Re: Cybernetics • Cliff Joslyn

CJ:

For a given arbitrary triadic relation (let’s say that and 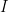are all finite, non‑empty sets), I’m interested to understand what additional axioms you’re saying are necessary and sufficient to make 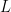a sign relation.  I checked Sign Relations • Definition, but it wasn’t obvious, or at least, not formalized.

Dear Cliff,

Peirce claims a definition of logic as formal semiotic and goes on to define a sign in terms of its relation to its interpretant sign and its object.

For ease of reference, here’s the cited paragraph again.

Logic will here be defined as formal semiotic.  A definition of a sign will be given which no more refers to human thought than does the definition of a line as the place which a particle occupies, part by part, during a lapse of time.  Namely, a sign is something, A, which brings something, B, its interpretant sign determined or created by it, into the same sort of correspondence with something, C, its object, as that in which itself stands to C.  It is from this definition, together with a definition of “formal”, that I deduce mathematically the principles of logic.  I also make a historical review of all the definitions and conceptions of logic, and show, not merely that my definition is no novelty, but that my non‑psychological conception of logic has virtually been quite generally held, though not generally recognized.  (C.S. Peirce, NEM 4, 20–21).

Let me cut to the chase and say what I see in that passage.  Peirce draws our attention to a category of mathematical structures of use in understanding various domains of complex phenomena by capturing aspects of objective structure immanent in those domains.

The domains of complex phenomena of interest to logic in its broadest sense encompass all that appears on the discourse side of any universe of discourse we happen to discuss.  That’s a big enough sky for anyone to live under, but for the moment I am focusing on the ways we transform signs in activities like communication, computation, inquiry, learning, proof, and reasoning in general.  I’m especially focused on the ways we do now and may yet use computation to advance the other pursuits on that list.

To be continued …

Reference

• Charles S. Peirce (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.

Sources

• C.S. Peirce • On the Definition of Logic
• C.S. Peirce • Logic as Semiotic
• C.S. Peirce • Objective Logic

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

A few items of notation are useful in discussing equivalence relations in general and semiotic equivalence relations in particular.

In general, if is an equivalence relation on a set then every element of belongs to a unique equivalence class under called the equivalence class of under .  Convention provides the square bracket notation for denoting such equivalence classes, in either the form or the simpler form when the subscript is understood.  A statement that the elements and are equivalent under is called an equation or an equivalence and may be expressed in any of the following ways.

Thus we have the following definitions.

In the application to sign relations it is useful to extend the square bracket notation in the following ways.  If is a sign relation whose connotative component is an equivalence relation on let be the equivalence class of under   In short,   A statement that the signs and belong to the same equivalence class under a semiotic equivalence relation is called a semiotic equation (SEQ) and may be written in either of the following forms.

In many situations there is one further adaptation of the square bracket notation for semiotic equivalence classes which can be useful.  Namely, when there is known to exist a particular triple in a sign relation it is permissible to let be defined as   This lets the notation for semiotic equivalence classes harmonize more smoothly with the frequent use of similar devices for the denotations of signs and expressions.

Applying the array of equivalence notations to the sign relations for and will serve to illustrate their use and utility.

The semiotic equivalence relation for interpreter yields the following semiotic equations.

or

In this way it induces the following semiotic partition.

The semiotic equivalence relation for interpreter yields the following semiotic equations.

or

In this way it induces the following semiotic partition.

References

• Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.
• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52.  Archive.  Journal.  Online (doc) (pdf).

Resources

• Inquiry
• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

Document History

See OEIS Wiki • Sign Relation • Document History.

cc: FB | Semeiotics • Cybernetics • Laws of Form • Ontolog Forum
cc: Conceptual Graphs • Structural Modeling • Systems Science

A semiotic equivalence relation (SER) is a special type of equivalence relation arising in the analysis of sign relations.  Generally speaking, any equivalence relation induces a partition of the underlying set of elements, known as the domain or space of the relation, into a family of equivalence classes.  In the case of a SER the equivalence classes are called semiotic equivalence classes (SECs) and the partition is called a semiotic partition (SEP).

The sign relations and have many interesting properties over and above those possessed by sign relations in general.  Some of those properties have to do with the relation between signs and their interpretant signs, as reflected in the projections of and on the ‑plane, notated as and respectively.  The dyadic relations on induced by those projections are also referred to as the connotative components of the corresponding sign relations, notated as and respectively.  Tables 6a and 6b show the corresponding connotative components.

A nice property of the sign relations and is that their connotative components and form a pair of equivalence relations on their common syntactic domain   This type of equivalence relation is called a semiotic equivalence relation (SER) because it equates signs having the same meaning to some interpreter.

Each of the semiotic equivalence relations, partitions the collection of signs into semiotic equivalence classes.  This constitutes a strong form of representation in that the structure of the interpreters’ common object domain is reflected or reconstructed, part for part, in the structure of each one’s semiotic partition of the syntactic domain

It’s important to observe the semiotic partitions for interpreters and are not identical, indeed, they are orthogonal to each other.  Thus we may regard the form of the partitions as corresponding to an objective structure or invariant reality, but not the literal sets of signs themselves, independent of the individual interpreter’s point of view.

Information about the contrasting patterns of semiotic equivalence corresponding to the interpreters and is summarized in Tables 7a and 7b.  The form of the Tables serves to explain what is meant by saying the SEPs for and are orthogonal to each other.

References

• Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.
• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52.  Archive.  Journal.  Online (doc) (pdf).

Resources

• Inquiry
• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

Document History

See OEIS Wiki • Sign Relation • Document History.

cc: FB | Semeiotics • Cybernetics • Laws of Form • Ontolog Forum
cc: Conceptual Graphs • Structural Modeling • Systems Science

A third aspect of a sign’s complete meaning concerns the relation between its objects and its interpretants, which has no standard name in semiotics.  It would be called an induced relation in graph theory or the result of relational composition in relation theory.  If an interpretant is recognized as a sign in its own right then its independent reference to an object can be taken as belonging to another moment of denotation, but this neglects the mediational character of the whole transaction in which this occurs.  Denotation and connotation have to do with dyadic relations in which the sign plays an active role but here we are dealing with a dyadic relation between objects and interpretants mediated by the sign from an off‑stage position, as it were.

As a relation between objects and interpretants mediated by a sign, this third aspect of meaning may be referred to as the ennotation of a sign and the dyadic relation making up the ennotative aspect of a sign relation may be notated as   Information about the ennotative aspect of meaning is obtained from by taking its projection on the object‑interpretant plane.  We may visualize this as the “shadow” casts on the 2‑dimensional space whose axes are the object domain and the interpretant domain   The ennotative component of a sign relation variously written in any of the forms,       and is defined as follows.

As it happens, the sign relations and are fully symmetric with respect to exchanging signs and interpretants, so all the data of is echoed unchanged in and all the data of is echoed unchanged in

Tables 5a and 5b show the ennotative components of the sign relations associated with the interpreters and respectively.  The rows of each Table list the ordered pairs in the corresponding projections,

References

• Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.
• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52.  Archive.  Journal.  Online (doc) (pdf).

Resources

• Inquiry
• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

Document History

See OEIS Wiki • Sign Relation • Document History.

cc: FB | Semeiotics • Cybernetics • Laws of Form • Ontolog Forum
cc: Conceptual Graphs • Structural Modeling • Systems Science

Another aspect of a sign’s complete meaning concerns the reference a sign has to its interpretants, which interpretants are collectively known as the connotation of the sign.  In the pragmatic theory of sign relations, connotative references fall within the projection of the sign relation on the plane spanned by its sign domain and its interpretant domain.

In the full theory of sign relations the connotative aspect of meaning includes the links a sign has to affects, concepts, ideas, impressions, intentions, and the whole realm of an interpretive agent’s mental states and allied activities, broadly encompassing intellectual associations, emotional impressions, motivational impulses, and real conduct.  Taken at the full, in the natural setting of semiotic phenomena, this complex system of references is unlikely ever to find itself mapped in much detail, much less completely formalized, but the tangible warp of its accumulated mass is commonly alluded to as the connotative import of language.

Formally speaking, however, the connotative aspect of meaning presents no additional difficulty.  The dyadic relation making up the connotative aspect of a sign relation is notated as   Information about the connotative aspect of meaning is obtained from by taking its projection on the sign-interpretant plane.  We may visualize this as the “shadow” casts on the 2-dimensional space whose axes are the sign domain and the interpretant domain   The connotative component of a sign relation variously written in any of the forms,       and is defined as follows.

Tables 4a and 4b show the connotative components of the sign relations associated with the interpreters and respectively.  The rows of each Table list the ordered pairs in the corresponding projections,

References

• Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.
• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52.  Archive.  Journal.  Online (doc) (pdf).

Resources

• Inquiry
• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

Document History

See OEIS Wiki • Sign Relation • Document History.

cc: FB | Semeiotics • Cybernetics • Laws of Form • Ontolog Forum
cc: Conceptual Graphs • Structural Modeling • Systems Science