Sign Relations • Examples

Posted on February 10, 2024 by Jon Awbrey

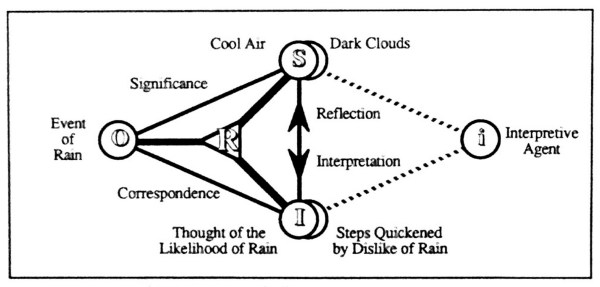
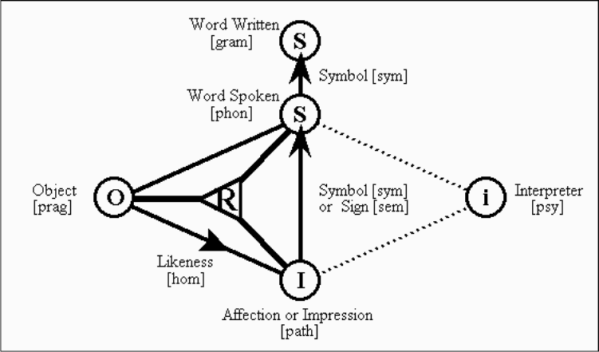
Soon after I made my third foray into grad school, this time in Systems Engineering, I was trying to explain sign relations to my advisor and he — being the very model of a modern systems engineer — asked me to give a concrete example of a sign relation, as simple as possible without being trivial.  After much cudgeling of the grey matter I came up with a pair of examples which had the added benefit of bearing instructive relationships to each other.  Despite their simplicity, the examples to follow have subtleties of their own and their careful treatment serves to illustrate important issues in the general theory of signs.

Imagine a discussion between two people, Ann and Bob, and attend only to the aspects of their interpretive practice involving the use of the following nouns and pronouns.

“Ann”,   “Bob”,   “I”,   “you”.

  • The object domain of their discussion is the set of two people \{ \text{Ann}, \text{Bob} \}.
  • The sign domain of their discussion is the set of four signs \{ {}^{\backprime\backprime} \text{Ann} {}^{\prime\prime}, {}^{\backprime\backprime} \text{Bob} {}^{\prime\prime}, {}^{\backprime\backprime} \text{I} {}^{\prime\prime}, {}^{\backprime\backprime} \text{you} {}^{\prime\prime} \}.

Ann and Bob are not only the passive objects of linguistic references but also the active interpreters of the language they use.  The system of interpretation (SOI) associated with each language user can be represented in the form of an individual three-place relation known as the sign relation of that interpreter.

In terms of its set-theoretic extension, a sign relation L is a subset of a cartesian product O \times S \times I.  The three sets O, S, I are known as the object domain, the sign domain, and the interpretant domain, respectively, of the sign relation L \subseteq O \times S \times I.

Broadly speaking, the three domains of a sign relation may be any sets at all but the types of sign relations contemplated in formal settings are usually constrained to having I \subseteq S.  In those cases it becomes convenient to lump signs and interpretants together in a single class called a sign system or syntactic domain.  In the forthcoming examples S and I are identical as sets, so the same elements manifest themselves in two different roles of the sign relations in question.

When it becomes necessary to refer to the whole set of objects and signs in the union of the domains O, S, I for a given sign relation L, we will call this set the World of L and write W = W_L = O \cup S \cup I.

To facilitate an interest in the formal structures of sign relations and to keep notations as simple as possible as the examples become more complicated, it serves to introduce the following general notations.

\begin{array}{ccl} O & = & \text{Object Domain} \\[6pt] S & = & \text{Sign Domain} \\[6pt] I & = & \text{Interpretant Domain} \end{array}

Introducing a few abbreviations for use in this Example, we have the following data.

\begin{array}{cclcl} O & = & \{ \text{Ann}, \text{Bob} \} & = & \{ \mathrm{A}, \mathrm{B} \} \\[6pt] S & = & \{ {}^{\backprime\backprime} \text{Ann} {}^{\prime\prime}, {}^{\backprime\backprime} \text{Bob} {}^{\prime\prime}, {}^{\backprime\backprime} \text{I} {}^{\prime\prime}, {}^{\backprime\backprime} \text{you} {}^{\prime\prime} \} & = & \{ {}^{\backprime\backprime} \mathrm{A} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{B} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{i} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{u} {}^{\prime\prime} \} \\[6pt] I & = & \{ {}^{\backprime\backprime} \text{Ann} {}^{\prime\prime}, {}^{\backprime\backprime} \text{Bob} {}^{\prime\prime}, {}^{\backprime\backprime} \text{I} {}^{\prime\prime}, {}^{\backprime\backprime} \text{you} {}^{\prime\prime} \} & = & \{ {}^{\backprime\backprime} \mathrm{A} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{B} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{i} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{u} {}^{\prime\prime} \} \end{array}

In the present example, S = I = \text{Syntactic Domain}.

Tables 1a and 1b show the sign relations associated with the interpreters \mathrm{A} and \mathrm{B}, respectively.  In this arrangement the rows of each Table list the ordered triples of the form (o, s, i) belonging to the corresponding sign relations, L_\mathrm{A}, L_\mathrm{B} \subseteq O \times S \times I.

Sign Relation Twin Tables LA & LB

The Tables codify a rudimentary level of interpretive practice for the agents \mathrm{A} and \mathrm{B} and provide a basis for formalizing the initial semantics appropriate to their common syntactic domain.  Each row of a Table lists an object and two co-referent signs, together forming an ordered triple (o, s, i) called an elementary sign relation, in other words, one element of the relation’s set-theoretic extension.

Already in this elementary context, there are several meanings which might attach to the project of a formal semiotics, or a formal theory of meaning for signs.  In the process of discussing the alternatives, it is useful to introduce a few terms occasionally used in the philosophy of language to point out the needed distinctions.  That is the task we’ll turn to next.

Resources

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Inquiry, Logic, Mathematics, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadicity | Tagged , , , , , , , , | 4 Comments

Sign Relations • Signs and Inquiry

Posted on February 9, 2024 by Jon Awbrey

There is a close relationship between the pragmatic theory of signs and the pragmatic theory of inquiry.  In fact, the correspondence between the two studies exhibits so many congruences and parallels it is often best to treat them as integral parts of one and the same subject.  In a very real sense, inquiry is the process by which sign relations come to be established and continue to evolve.  In other words, inquiry, “thinking” in its best sense, “is a term denoting the various ways in which things acquire significance” (Dewey, 38).

Tracing the passage of inquiry through the medium of signs calls for an active, intricate form of cooperation between our converging modes of investigation.  Its proper character is best understood by realizing the theory of inquiry is adapted to study the developmental aspects of sign relations, whose evolution the theory of signs is specialized to treat from comparative and structural points of view.

References

  • Dewey, J. (1910), How We Think, D.C. Heath, Boston, MA.  Reprinted (1991), Prometheus Books, Buffalo, NY.  Online.
  • Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52.  Archive.  Journal.  Online (doc) (pdf).

Resources

Document History

See OEIS Wiki • Sign Relation • Document History

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Inquiry, Logic, Mathematics, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadicity | Tagged , , , , , , , , | 4 Comments

Sign Relations • Definition

Posted on February 8, 2024 by Jon Awbrey

One of Peirce’s clearest and most complete definitions of a sign is one he gives in the context of providing a definition for logic, and so it is informative to view it in that setting.

Logic will here be defined as formal semiotic.  A definition of a sign will be given which no more refers to human thought than does the definition of a line as the place which a particle occupies, part by part, during a lapse of time.  Namely, a sign is something, A, which brings something, B, its interpretant sign determined or created by it, into the same sort of correspondence with something, C, its object, as that in which itself stands to C.  It is from this definition, together with a definition of “formal”, that I deduce mathematically the principles of logic.  I also make a historical review of all the definitions and conceptions of logic, and show, not merely that my definition is no novelty, but that my non-psychological conception of logic has virtually been quite generally held, though not generally recognized.  (C.S. Peirce, NEM 4, 20–21).

In the general discussion of diverse theories of signs, the question frequently arises whether signhood is an absolute, essential, indelible, or ontological property of a thing, or whether it is a relational, interpretive, and mutable role a thing can be said to have only within a particular context of relationships.

Peirce’s definition of a sign defines it in relation to its object and its interpretant sign, and thus defines signhood in relative terms, by means of a predicate with three places.  In this definition, signhood is a role in a triadic relation, a role a thing bears or plays in a given context of relationships — it is not an absolute, non‑relative property of a thing‑in‑itself, a status it maintains independently of all relationships to other things.

Some of the terms Peirce uses in his definition of a sign may need to be elaborated for the contemporary reader.

  • Correspondence.  From the way Peirce uses this term throughout his work it is clear he means what he elsewhere calls a “triple correspondence”, in short, just another way of referring to the whole triadic sign relation itself.  In particular, his use of this term should not be taken to imply a dyadic correspondence, as in the varieties of “mirror image” correspondence between realities and representations bandied about in contemporary controversies about “correspondence theories of truth”.
  • Determination.  Peirce’s concept of determination is broader in several ways than the sense of the word referring to strictly deterministic causal‑temporal processes.  First, and especially in this context of defining logic, he uses a more general concept of determination, what is known as formal or informational determination, as we use in geometry when we say “two points determine a line”, rather than the more special cases of causal or temporal determinisms.  Second, he characteristically allows for the broader concept of determination in measure, that is, an order of determinism admitting a full spectrum of more and less determined relationships.
  • Non‑Psychological.  Peirce’s “non‑psychological conception of logic” must be distinguished from any variety of anti‑psychologism.  He was quite interested in matters of psychology and had much of import to say about them.  But logic and psychology operate on different planes of study even when they happen to view the same data, as logic is a normative science where psychology is a descriptive science.  Thus they have distinct aims, methods, and rationales.

Reference

  • Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.

Resources

Document History

See OEIS Wiki • Sign Relation • Document History

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Inquiry, Logic, Mathematics, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadicity | Tagged , , , , , , , , | 4 Comments

Sign Relations • Anthesis

Posted on February 7, 2024 by Jon Awbrey

Thus, if a sunflower, in turning towards the sun, becomes by that very act fully capable, without further condition, of reproducing a sunflower which turns in precisely corresponding ways toward the sun, and of doing so with the same reproductive power, the sunflower would become a Representamen of the sun.

— C.S. Peirce, Collected Papers, CP 2.274

In his picturesque illustration of a sign relation, along with his tracing of a corresponding sign process, or semiosis, Peirce uses the technical term representamen for his concept of a sign, but the shorter word is precise enough, so long as one recognizes its meaning in a particular theory of signs is given by a specific definition of what it means to be a sign.

Resources

Document History

Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Inquiry, Logic, Mathematics, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadicity | Tagged , , , , , , , , | 4 Comments

Interpreter and Interpretant • Discussion 4

Posted on February 6, 2024 by Jon Awbrey

Re: Interpreter and Interpretant • Selection 4

Dewey's “Sign of Rain” Example
\text{Figure 2. Dewey's ``Sign of Rain" Example}

Re: Conceptual Graphs • Tom Gollier

Tom,

Another discussion coming to mind is one we had on this subject in 2016.  Once again I’ll save a measure of strain on my brain by reprising that here and picking up from that point.

Re: Peirce List • Abduction, Deduction, Induction : Analogy, Inquiry • Tom Gollier

I know we’ve discussed the various meanings of the word object which make sense in Peirce’s semiotics and pragmatism generally, so let me just link to a recent comment I found in my search for previous mentions.

Objects, Objectives, Objectivity

I am constantly reminded of the following line from Peirce.

“No longer wondered what I would do in life but defined my object.”
— C.S. Peirce (1861), “My Life, written for the Class-Book”, (CE 1, 3)

The question of Objects, Objectives, and Objectivity is a persistent one.

The Latin-rooted English object springs from deeper roots in the Greek pragma.  It was a personal revelation to me on first looking into Liddell and Scott and reading all the meanings and ramifications of that vast pragmatic semantic complex.

It is especially the senses of the word object referring to aims and purposes, in other words, intentional objects and objects of intention, that we are likely to miss if we don’t remind ourselves of their pertinence to pragmatic thinking.

Keeping that variety of meanings in mind, a few more words may help to clarify the reading from last time.

  • There are of course the usual run of behaviorist, causal, stimulus-response theories of “signal processing” and “verbal behavior” that have enjoyed their popularity and never-say-die revivals from the days of Charles Morris to B.F. Skinner, but Peirce’s semiotics includes them as degenerate species of the more solid genre he had in mind.
  • Peirce’s definition of a triadic sign relation is cast at such a level of generality that nothing in it prevents a sign relation L \subseteq O \times S \times I from having intentional objects in its object domain O.
  • To say that coolness is a sign of rain is a perfectly natural statement in English and I think it would be a more troubling narrowness to exclude it from sense.
  • Semiotic objects are any objects of discussion or thought.  It should be obvious that we talk and think about future, imaginary, intentional, or “virtual” objects all the time.
  • The fact that coolness might be a sign of many other things is exactly what calls for our peripatetic hero to abduce a hypothesis (rain?), to deduce a prediction (dark clouds?), and to test the prediction against further observations (look up!).  All of those features are why we chose Dewey’s story as an illustration of a full-blown inquiry.

Reference

It helps to read “object” in a fuller sense than we often do in billiard‑ball philosophies, as a lot gets lost in the translation from the Greek “pragma” from which pragmatism naturally takes its cue.  For a sample of that fuller sense see the following lexicon entry.

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Diagrammatic Reasoning, Interpretive Frameworks, Logic, Logical Graphs, Objective Frameworks, Relation Theory, Semiotics, Sign Relations, Systems of Interpretation, Triadic Relations, Visualization | Tagged , , , , , , , , , , , | 4 Comments

Interpreter and Interpretant • Discussion 3

Posted on February 5, 2024 by Jon Awbrey

Re: Interpreter and Interpretant • Selection 4

Dewey's “Sign of Rain” Example
\text{Figure 2. Dewey's ``Sign of Rain" Example}

Re: Conceptual Graphs • Tom Gollier

TG:
Given your diagram of Dewey’s example, I don’t see how the event of rain can be the object (O).  The objects seem more clearly to be the air and the clouds which in their coolness and darkness are being taken as signs (S).  The event of rain is only included in this situation via the interpretant (I), the thought to the likelihood of rain.

What’s more, the ambiguity of this interpretant, being both a thought of the likelihood of rain and the object, rain, might be a clue to getting at the nature of the interpretant in general as we move along?

Tom,

The meaning of the word object in pragmatic thought is another one of those topics we keep circling back to.  There are more thought‑out thoughts I shared in my early days on the Peirce List, but since this very issue arose just recently in other discussions I’ll save myself a modicum of mental effort by linking to my latest attempts to clarify the point.

The object of reasoning is to find out …

No longer wondered what I would do in life but defined my object.
— C.S. Peirce (1861), “My Life, written for the Class-Book”, (CE 1, 3)

The object of reasoning is to find out, from the consideration of what we already know, something else which we do not know.
— C.S. Peirce (1877), “The Fixation of Belief”, (CP 5.365)

If the object of an investigation is to find out something we do not know then the clues we discover along the way are the signs which determine that object.

People will continue to be confused about determination so long as they can think of no other forms but analytic-behaviorist-causal-dyadic-temporal, object-as-stimulus, sign-as-response varieties.  It’s true ordinary language biases us toward billiard‑ball styles of dyadic determination but there are triadic forms of constraint, determination, and interaction not captured by S‑R chains of that order.

Pragmatic objects of signs and concepts are anything we talk or think about and semiosis does not conduct its transactions within the bounds of object as cue, sign as cue ball, and interpretants as solids, stripes, and pockets.

References

  • Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52.  Archive.  Journal.  Online (doc) (pdf).
  • Dewey, J. (1910/1991), How We Think, D.C. Heath, Boston, MA.  Reprinted (1991), Prometheus Books, Buffalo, NY.  Online.
  • Peirce, C.S. (1859–1861), “My Life, written for the Class-Book”, pp. 1–3 in Writings of Charles S. Peirce : A Chronological Edition, Volume 1, 1857–1866, Peirce Edition Project, Indiana University Press, Bloomington, IN, 1982.
  • Peirce, C.S. (1877), “The Fixation Of Belief”, Popular Science Monthly 12 (Nov 1877), pp. 1–15.  Reprinted in Collected Papers, CP 5.358–387.  Online.

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Diagrammatic Reasoning, Interpretive Frameworks, Logic, Logical Graphs, Objective Frameworks, Relation Theory, Semiotics, Sign Relations, Systems of Interpretation, Triadic Relations, Visualization | Tagged , , , , , , , , , , , | 4 Comments

Interpreter and Interpretant • Discussion 2

Posted on February 3, 2024 by Jon Awbrey

Re: Interpreter and Interpretant • Selection 1

Sign Relation in Aristotle
\text{Figure 1. The Sign Relation in Aristotle}

Re: Laws of Form • Lyle Anderson

LA:
You can not find “ground” in Aristotle.  If the past three years have shown us anything it is that his assertion:

But the mental affections themselves, of which these words are primarily signs (semeia), are the same for the whole of mankind, as are also the objects (pragmata) of which those affections are representations or likenesses, images, copies (homoiomata).

Is just plain wrong.  The whole of mankind does not have the same “mental affectations”, some are sane and some are insane.

Lyle,

What prompted the present review of basic issues in semiotics was a couple of recent instances where one of the most nagging questions in the whole field reared its shaggy head again.  This time around I posed it as follows.

In a theory of three‑place relations among objects, signs, and interpretant signs, where indeed is there any place for the interpretive agent?

It’s best to take the Selections I gathered not as Scripture but as case studies in the conduct of inquiry where the inquirers in question managed to capture significant features of the way triadic sign relations structure the phenomena of cognition, communication, and computation.  No one in science gets everything right all the time, much less at first, but first approximations taken for what they’re worth prime the pump of stepwise refinement in semiotics as in computer science.

In that spirit, Susan Awbrey and I summed up our estimation of Aristotle’s Approximation to the Sign Relation in the following way.

Aristotle’s description contains two claims of constancy, that ideas and objects are the same for all interpreters.  This view does not allow for the plurality and mutability of interpreters, two features that we must be concerned with in hermeneutics and education.  John Dewey expresses this point well:

Thinking is specific, in that different things suggest their own appropriate meanings, tell their own unique stories, and in that they do this in very different ways with different persons.  (Dewey 1910/1991, 39).

However, this account of Aristotle’s may be considered in part a reasonable approximation and in part a suggestive metaphor, suitable as a first approach to a complex subject.  (Awbrey and Awbrey, 1995).

References

  • Aristotle, “On Interpretation” (De Interp.), Harold P. Cooke (trans.), pp. 111–179 in Aristotle, Volume 1, Loeb Classical Library, William Heinemann, London, UK, 1938.
  • Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52.  Archive.  Journal.  Online (doc) (pdf).

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Diagrammatic Reasoning, Interpretive Frameworks, Logic, Logical Graphs, Objective Frameworks, Relation Theory, Semiotics, Sign Relations, Systems of Interpretation, Triadic Relations, Visualization | Tagged , , , , , , , , , , , | 4 Comments

Interpreter and Interpretant • Discussion 1

Posted on February 1, 2024 by Jon Awbrey

Re: Conceptual Graphs • Helmut Raulien  

HR:
I find it a bit problematic to say, that the sign determines the interpretant, because the sign doesn’t infer, it is the interpreter, who does the inference.  But ok, I guess we might say, that Peirce prescinds the semiosis from the interpreter, so, ok, the flow of determination goes from the sign to the interpretant, because it is the interpreter, who receives the sign, and then forms the interpretant […]

Helmut,

Thanks for this.  Something about the way you expressed the question led me to think of a new angle on it.

What makes an interpretant is fairly simple, at least, here’s the catch, once you have the appropriate mathematical framework in place — An interpretant is whatever appears in the third place of a sign‑relational triple (o, s, i).

What makes an interpreter is more complex.  I’ll take that up as I get more time.

Resources

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Diagrammatic Reasoning, Interpretive Frameworks, Logic, Logical Graphs, Objective Frameworks, Relation Theory, Semiotics, Sign Relations, Systems of Interpretation, Triadic Relations, Visualization | Tagged , , , , , , , , , , , | 4 Comments

Interpreter and Interpretant • Selection 4

Posted on January 31, 2024 by Jon Awbrey

Interpretation and Inquiry

To illustrate the role of sign relations in inquiry we begin with Dewey’s elegant and simple example of reflective thinking in everyday life.

A man is walking on a warm day.  The sky was clear the last time he observed it;  but presently he notes, while occupied primarily with other things, that the air is cooler.  It occurs to him that it is probably going to rain;  looking up, he sees a dark cloud between him and the sun, and he then quickens his steps.  What, if anything, in such a situation can be called thought?  Neither the act of walking nor the noting of the cold is a thought.  Walking is one direction of activity;  looking and noting are other modes of activity.  The likelihood that it will rain is, however, something suggested.  The pedestrian feels the cold;  he thinks of clouds and a coming shower.

(John Dewey, How We Think, 6–7)

In Dewey’s narrative we can identify the characters of the sign relation as follows.  Coolness is a Sign of the Object rain, and the Interpretant is the thought of the rain’s likelihood.  In his description of reflective thinking Dewey distinguishes two phases, “a state of perplexity, hesitation, doubt” and “an act of search or investigation” (p. 9), comprehensive stages which are further refined in his later model of inquiry.

Reflection is the action the interpreter takes to establish a fund of connections between the sensory shock of coolness and the objective danger of rain by way of the impression rain is likely.  But reflection is more than irresponsible speculation.  In reflection the interpreter acts to charge or defuse the thought of rain by seeking other signs the thought implies and evaluating the thought according to the results of that search.

Figure 2 shows the semiotic relationships involved in Dewey’s story, tracing the structure and function of the sign relation as it informs the activity of inquiry, including both the movements of surprise explanation and intentional action.  The labels on the outer edges of the sign‑relational triple suggest the significance of signs for eventual occurrences and the correspondence of ideas with external orientations.  But there is nothing essential about the dyadic role distinctions they imply, as it is only in special or degenerate cases that such projections preserve enough information to determine the original sign relation.

Dewey's “Sign of Rain” Example
\text{Figure 2. Dewey's ``Sign of Rain" Example}

References

  • Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52.  Archive.  Journal.  Online (doc) (pdf).
  • Dewey, J. (1910), How We Think, D.C. Heath, Boston, MA.  Reprinted (1991), Prometheus Books, Buffalo, NY.  Online.

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Diagrammatic Reasoning, Interpretive Frameworks, Logic, Logical Graphs, Objective Frameworks, Relation Theory, Semiotics, Sign Relations, Systems of Interpretation, Triadic Relations, Visualization | Tagged , , , , , , , , , , , | 4 Comments

Interpreter and Interpretant • Selection 3

Posted on January 30, 2024 by Jon Awbrey

The following selection from Peirce’s “Lowell Lectures on the Logic of Science” (1866) lays out in detail his “metaphorical argument” for the relationship between interpreters and interpretant signs.

I think we need to reflect upon the circumstance that every word implies some proposition or, what is the same thing, every word, concept, symbol has an equivalent term — or one which has become identified with it, — in short, has an interpretant.

Consider, what a word or symbol is;  it is a sort of representation.  Now a representation is something which stands for something.  I will not undertake to analyze, this evening, this conception of standing for something — but, it is sufficiently plain that it involves the standing to something for something.  A thing cannot stand for something without standing to something for that something.  Now, what is this that a word stands to?  Is it a person?

We usually say that the word homme stands to a Frenchman for man.  It would be a little more precise to say that it stands to the Frenchman’s mind — to his memory.  It is still more accurate to say that it addresses a particular remembrance or image in that memory.  And what image, what remembrance?  Plainly, the one which is the mental equivalent of the word homme — in short, its interpretant.  Whatever a word addresses then or stands to, is its interpretant or identified symbol.  […]

The interpretant of a term, then, and that which it stands to are identical.  Hence, since it is of the very essence of a symbol that it should stand to something, every symbol — every word and every conception — must have an interpretant — or what is the same thing, must have information or implication.  (Peirce 1866, Chronological Edition 1, pp. 466–467).

Reference

  • Peirce, C.S. (1866), “The Logic of Science, or, Induction and Hypothesis”, Lowell Lectures of 1866, pp. 357–504 in Writings of Charles S. Peirce : A Chronological Edition, Volume 1, 1857–1866, Peirce Edition Project, Indiana University Press, Bloomington, IN, 1982.

Resource

cc: FB | Semeiotics • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Diagrammatic Reasoning, Interpretive Frameworks, Logic, Logical Graphs, Objective Frameworks, Relation Theory, Semiotics, Sign Relations, Systems of Interpretation, Triadic Relations, Visualization | Tagged , , , , , , , , , , , | 3 Comments