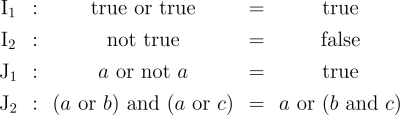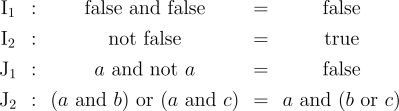Re: Logical Graphs • Formal Development
Re: Laws of Form • Armahedi Mahzar
- AM:
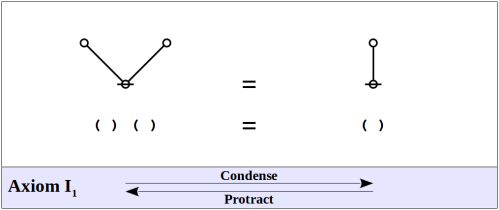
- GSB took J1 : (a(a)) = as the first algebraic primitive and the second one is transposition so he only need only 2 primitives for the primary algebra.
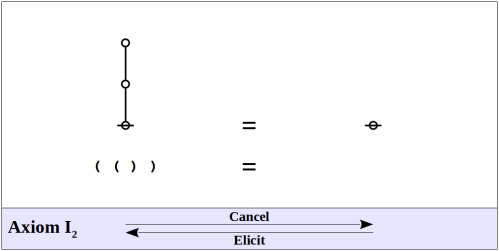
Reflexion ((a)) = a is proven without using Cancellation (( )) = .
In fact, he can prove cancellation from C1 reflexion.
Condensation ( )( ) = ( ) can be derived from C4 iteration.
So, his algebra is simpler from your Cactus Calculus.
Dear Arma,
I had a feeling we’ve discussed this before, and probably in a lot more detail than I have time for at the moment, so I hunted up the previous discussion — turns out it was on the old Yahoo Group — there’s a copy of that below for whatever memory‑jogging it may be worth.
To my way of thinking, what you say about reducing the primary arithmetic to the primary algebra shows a lack of appreciation for the fundamental nature of that distinction. Indeed, the recognition and clarification of that distinction is one of the most important upgrades Spencer Brown added to Peirce’s initial systems of logical graphs.
As far as the other score goes, the advantages of handling label changes and structure changes separately in one’s syntactic operations is just one of those things I learned in the hard knocks way of programming theorem provers for logical graphs, and I all I can do is keep recommending it on that account.
Regards,
Jon
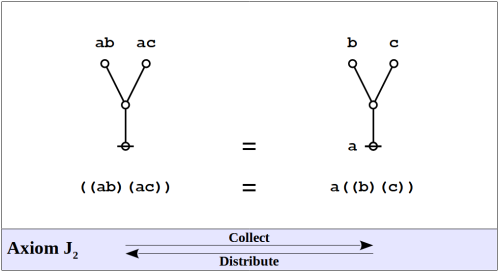
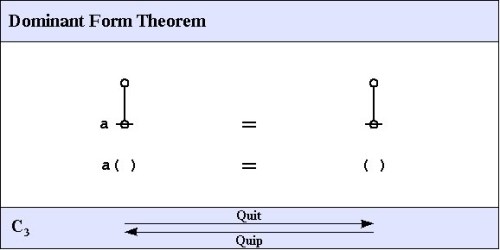
From: Jon Awbrey To: Yahoo Laws Of Form Date: 8/15/2017, 2:10 PM Re: Peirce's Law Arma, All ... Re: https://intersci.ss.uci.edu/wiki/index.php/Logical_graph#Axioms Let me try a few ascii graphics to see how this site treats them. It's clear that the two systems are equivalent, since we have: a a o---o | @ =======J1′ [delete] o---o | @ =======I2 [cancel] @ =======QED J1 For my part, I am less concerned with small differences in the lengths of proofs than I am with other factors. It's hard for me to remember all the reasons for decisions I made 40 years ago — as a general rule, Peirce's way of looking at the relation between mathematics and logic was and still is very influential and the other main impact came from the nuts @ and bolts | requirements of computational representation. But looking at the choice with present eyes, I think I would continue to prefer the I1, I2, J1′, J2 system over the alternative simply for the fact that it treats two different types of operation separately, namely, changes in formal or graphical structure versus changes in the occurrence or placement of variables. Regards, Jon On 8/14/2017 11:01 PM, armahedi@yahoo.com [lawsofform] wrote: > Hi Jon > > With your answer > 'Recall that I am using “p(p)=( )” for my J1. > I can go back to calling it J1′ if need be.', > I realize that your axiom system is different from > Brownian Primary Algebra. > > Here is your axioms > I1 ()()=() > I2 (())= > J1' (a)a=( ) > J2 ((ab)(ac))=a((b)c) > and these are Spencer-Brown axioms > J1 ((a)a)= > J2 ((ab)(ac))=a((b)(c)) > > From these axioms you derived three theorems which are > identical to the first Spencer-Brown Primary Algebra > consequences: Reflection, Generation and Integration. > > Here are your proofs in parentheses notation with > my critical observations. > > You prove Reflection ((a))=a in 8 steps > ((a)) > =((a))(( )) I2 > =((a))(( (a))( a))) J1' > = ((((a))(a))(((a))a))) J2 > = (( )(((a))a))) J1' > = ((( a ) a )(((a))a))) J1' > = a((( a ) )(((a)) ))) J2 > = a(( )) J1' > = a I2 > while in Brownian Primary Algebra the proof is only 6 steps > because I2+J1'=J1'+I2=J1 > > You proved Generation (a)b=(ab)b in 5 steps > (a)b > =(((a)b)) C1 > =(((a)b))(( )) I2 > =(((a)b))((b)b)) J1' > =((a))((b)))b J2 > =(ab)b C1 > while in Brownian Primary Algebra the proof is only 4 steps > because I2+J1'=J1. > > You proved Integration a( )=( ) in 2 steps > a( ) > =a(a) C2 > =( ) J1' > While in Brownian Primary Algebra the proof is 3 steps > because it needs another step C1 > a( ) > =a(a) C2 > =((a(a))) C1 > =( ) J1 > > Comparing the proofs it seems to me that Brownian proof is better > because it does not need the arithmetical primitives I1 and I2. > > The beauty is that the arithmetical primitives become derived > theorems in Brownian Primary Algebra. I2 is J1 with x= dan > I1 is the 4th consequence xx=x with x=( ). So Brownian Primary > algebra is more economic than your algebra. > > However, it is just my subjective aesthetical preference, your > logical superstructure (cactus calculus, differential logic and > dynamical logic) is still intact fortunately. > > Please correct me if I am wrong. > Thanks > Arma
cc: FB | Logical Graphs • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
have the form of equations. This means the inference steps they license are reversible. The proof annotation scheme employed below makes use of double bars 
to mark this fact, though it will often be left to the reader to decide which of the two possible directions is the one required for applying the indicated axiom.
![\begin{array}{ccccc} \mathrm{I_1} & : & \text{true} ~ \text{or} ~ \text{true} & = & \text{true} \\[4pt] \mathrm{I_2} & : & \text{not} ~ \text{true} & = & \text{false} \\[4pt] \mathrm{J_1} & : & a ~ \text{or} ~ \text{not} ~ a & = & \text{true} \\[4pt] \mathrm{J_2} & : & (a ~ \text{or} ~ b) ~ \text{and} ~ (a ~ \text{or} ~ c) & = & a ~ \text{or} ~ (b ~ \text{and} ~ c) \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bccccc%7D++%5Cmathrm%7BI_1%7D++%26+%3A+%26+%5Ctext%7Btrue%7D+%7E+%5Ctext%7Bor%7D+%7E+%5Ctext%7Btrue%7D++%26+%3D+%26+%5Ctext%7Btrue%7D++%5C%5C%5B4pt%5D++%5Cmathrm%7BI_2%7D++%26+%3A+%26+%5Ctext%7Bnot%7D+%7E+%5Ctext%7Btrue%7D++%26+%3D+%26+%5Ctext%7Bfalse%7D++%5C%5C%5B4pt%5D++%5Cmathrm%7BJ_1%7D++%26+%3A+%26+a+%7E+%5Ctext%7Bor%7D+%7E+%5Ctext%7Bnot%7D+%7E+a++%26+%3D+%26+%5Ctext%7Btrue%7D++%5C%5C%5B4pt%5D++%5Cmathrm%7BJ_2%7D++%26+%3A+%26+%28a+%7E+%5Ctext%7Bor%7D+%7E+b%29+%7E+%5Ctext%7Band%7D+%7E+%28a+%7E+%5Ctext%7Bor%7D+%7E+c%29++%26+%3D+%26+a+%7E+%5Ctext%7Bor%7D+%7E+%28b+%7E+%5Ctext%7Band%7D+%7E+c%29++%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=1&c=20201002)
![\begin{array}{ccccc} \mathrm{I_1} & : & \text{false} ~ \text{and} ~ \text{false} & = & \text{false} \\[4pt] \mathrm{I_2} & : & \text{not} ~ \text{false} & = & \text{true} \\[4pt] \mathrm{J_1} & : & a ~ \text{and} ~ \text{not} ~ a & = & \text{false} \\[4pt] \mathrm{J_2} & : & (a ~ \text{and} ~ b) ~ \text{or} ~ (a\ \text{and}\ c) & = & a ~ \text{and} ~ (b ~ \text{or} ~ c) \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bccccc%7D++%5Cmathrm%7BI_1%7D++%26+%3A+%26+%5Ctext%7Bfalse%7D+%7E+%5Ctext%7Band%7D+%7E+%5Ctext%7Bfalse%7D++%26+%3D+%26+%5Ctext%7Bfalse%7D++%5C%5C%5B4pt%5D++%5Cmathrm%7BI_2%7D++%26+%3A+%26+%5Ctext%7Bnot%7D+%7E+%5Ctext%7Bfalse%7D++%26+%3D+%26+%5Ctext%7Btrue%7D++%5C%5C%5B4pt%5D++%5Cmathrm%7BJ_1%7D++%26+%3A+%26+a+%7E+%5Ctext%7Band%7D+%7E+%5Ctext%7Bnot%7D+%7E+a+++%26+%3D+%26+%5Ctext%7Bfalse%7D++%5C%5C%5B4pt%5D++%5Cmathrm%7BJ_2%7D++%26+%3A+%26+%28a+%7E+%5Ctext%7Band%7D+%7E+b%29+%7E+%5Ctext%7Bor%7D+%7E+%28a%5C+%5Ctext%7Band%7D%5C+c%29++%26+%3D+%26+a+%7E+%5Ctext%7Band%7D+%7E+%28b+%7E+%5Ctext%7Bor%7D+%7E+c%29++%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=1&c=20201002)
Inquiry Into Inquiry 