Differential Logic

Tangent and Remainder Maps

If we follow the classical line which singles out linear functions as ideals of simplicity then we may complete the analytic series of the proposition $f = pq : X \to \mathbb{B}$ in the following way.

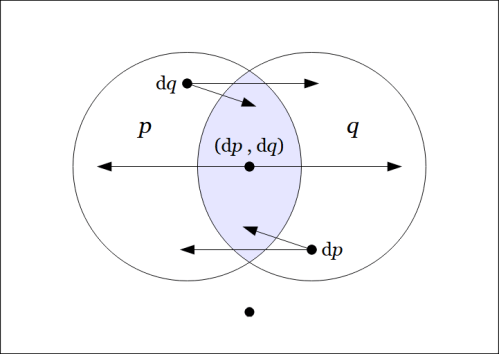
The next venn diagram shows the differential proposition $\mathrm{d}f = \mathrm{d}(pq) : \mathrm{E}X \to \mathbb{B}$ we get by extracting the linear approximation to the difference map $\mathrm{D}f = \mathrm{D}(pq) : \mathrm{E}X \to \mathbb{B}$ at each cell or point of the universe $X.$ What results is the logical analogue of what would ordinarily be called the differential of $pq$ but since the adjective differential is being attached to just about everything in sight the alternative name tangent map is commonly used for $\mathrm{d}f$ whenever it’s necessary to single it out.

$\text{Tangent Map}~ \mathrm{d}(pq) : \mathrm{E}X \to \mathbb{B}$

To be clear about what’s being indicated here, it’s a visual way of summarizing the following data.

$\begin{array}{rcccccc} \mathrm{d}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \mathrm{d}p \texttt{,} \mathrm{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \mathrm{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \mathrm{d}p \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & 0 \end{array}$

To understand the extended interpretations, that is, the conjunctions of basic and differential features which are being indicated here, it may help to note the following equivalences.

$\begin{matrix} \texttt{(} \mathrm{d}p \texttt{,} \mathrm{d}q \texttt{)} & = & \texttt{~} \mathrm{d}p \texttt{~} \texttt{(} \mathrm{d}q \texttt{)} & + & \texttt{(} \mathrm{d}p \texttt{)} \texttt{~} \mathrm{d}q \texttt{~} \\[4pt] dp & = & \texttt{~} \mathrm{d}p \texttt{~} \texttt{~} \mathrm{d}q \texttt{~} & + & \texttt{~} \mathrm{d}p \texttt{~} \texttt{(} \mathrm{d}q \texttt{)} \\[4pt] \mathrm{d}q & = & \texttt{~} \mathrm{d}p \texttt{~} \texttt{~} \mathrm{d}q \texttt{~} & + & \texttt{(} \mathrm{d}p \texttt{)} \texttt{~} \mathrm{d}q \texttt{~} \end{matrix}$

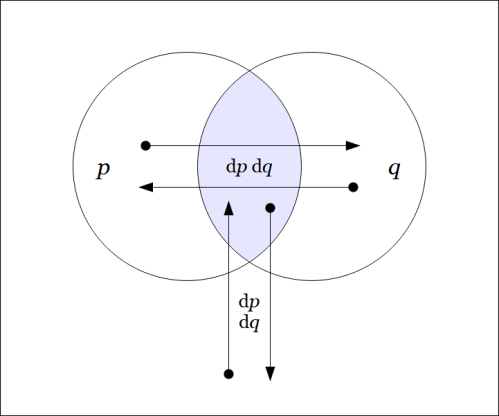
Capping the analysis of the proposition $pq$ in terms of succeeding orders of linear propositions, the final venn diagram of the series shows the remainder map $\mathrm{r}(pq) : \mathrm{E}X \to \mathbb{B},$ which happens to be linear in pairs of variables.

$\text{Remainder}~ \mathrm{r}(pq) : \mathrm{E}X \to \mathbb{B}$

Reading the arrows off the map produces the following data.

$\begin{array}{rcccccc} \mathrm{r}(pq) & = & p & \cdot & q & \cdot & \mathrm{d}p ~ \mathrm{d}q \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \mathrm{d}p ~ \mathrm{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \mathrm{d}p ~ \mathrm{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \mathrm{d}p ~ \mathrm{d}q \end{array}$

In short, $\mathrm{r}(pq)$ is a constant field, having the value $\mathrm{d}p~\mathrm{d}q$ at each cell.

Resources

cc: Academia.edu • Cybernetics • Structural Modeling • Systems Science
cc: Conceptual Graphs • Laws of Form • Ma^thstodon • Research Gate

	Survey of Semiotics,… on Sign Relations • Examples
	Sign Relations • Exa… on Survey of Semiotics, Semiosis,…
	Sign Relations • Sig… on Survey of Inquiry Driven Syste…
	Sign Relations • Sig… on Survey of Inquiry Driven Syste…
	Sign Relations • Sig… on Survey of Semiotics, Semiosis,…
	Survey of Semiotics,… on Sign Relations • Signs and…
	Sign Relations • Sig… on Survey of Semiotics, Semiosis,…
	Sign Relations • Def… on Survey of Semiotics, Semiosis,…
	Survey of Semiotics,… on Sign Relations • Definiti…
	Sign Relations • Def… on Survey of Semiotics, Semiosis,…

M	T	W	T	F	S	S
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30