Grammar 1 (concl.)
Returning to the case of the cactus language, the process of recognizing iterative or recursive types can be illustrated in the following way. The operative phrases in the simplest form of recursive definition are its initial part and its generic part. For the cactus language one has the following definitions of concatenation as iterated precatenation and surcatenation as iterated subcatenation, respectively.
Transforming the recursive definitions into grammar rules is accomplished by introducing a new pair of intermediate symbols, and
corresponding to the operations of the same names but ignoring the inflexions of their individual parameters
and
Recognizing the type of a sentence by means of the initial symbol
and interpreting
and
as names for the types of strings generated by concatenation and by surcatenation, respectively, one arrives at the following transformation of the ruling operator definitions into the form of covering grammar rules.
The draft of a grammar reached at this point represents a measure of improvement. Still, it exhibits a couple of features which are desirable to amend.
- Given the covering
the covering rule
says no more than the covering rule
Consequently, all the information contained in those two covering rules is already covered by the statement that
- Grammar rules invoking notions of discatenation, deletion, erasure, and other forms of retrograde production may be felt to lack due elegance. If for the sake of the aesthetic in question one entertains for a moment keeping open the option of adopting that style of critique, it becomes necessary to backtrack a little bit, to experiment with withdrawing all forms of elliptical operators, but without, of course, eliding the record of having considered them.
Resources
cc: Academia.edu • BlueSky • Laws of Form • Mathstodon • Research Gate
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science


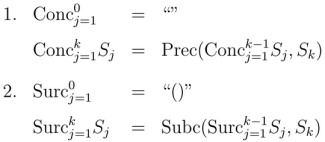
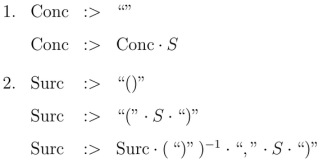
Pingback: Survey of Animated Logical Graphs • 8 | Inquiry Into Inquiry
Pingback: Survey of Animated Logical Graphs • 8 | Systems Community of Inquiry