Differential Logic

Field Picture

Let us summarize the outlook on differential logic we’ve reached so far. We’ve been considering a class of operators on universes of discourse, each of which takes us from considering one universe of discourse $X^\bullet$ to considering a larger universe of discourse $\mathrm{E}X^\bullet.$ An operator $\mathrm{W}$ of that general type, namely, $\mathrm{W} : X^\bullet \to \mathrm{E}X^\bullet,$ acts on each proposition $f : X \to \mathbb{B}$ of the source universe ${X^\bullet}$ to produce a proposition $\mathrm{W}f : \mathrm{E}X \to \mathbb{B}$ of the target universe $\mathrm{E}X^\bullet.$

The operators we’ve examined so far are the enlargement or shift operator $\mathrm{E} : X^\bullet \to \mathrm{E}X^\bullet$ and the difference operator $\mathrm{D} : X^\bullet \to \mathrm{E}X^\bullet.$ The operators $\mathrm{E}$ and $\mathrm{D}$ act on propositions in $X^\bullet,$ that is, propositions of the form $f : X \to \mathbb{B}$ which amount to propositions about the subject matter of $X,$ and they produce propositions of the form $\mathrm{E}f, \mathrm{D}f : \mathrm{E}X \to \mathbb{B}$ which amount to propositions about specified collections of changes conceivably occurring in $X.$

At this point we find ourselves in need of visual representations, suitable arrays of concrete pictures to anchor our more earthy intuitions and help us keep our wits about us as we venture into ever more rarefied airs of abstraction.

One good picture comes to us by way of the field concept. Given a space $X,$ a field of a specified type $Y$ over $X$ is formed by associating with each point of $X$ an object of type $Y.$ If that sounds like the same thing as a function from $X$ to the space of things of type $Y$ — it is nothing but — and yet it does seem helpful to vary the mental images and take advantage of the figures of speech most naturally springing to mind under the emblem of the field idea.

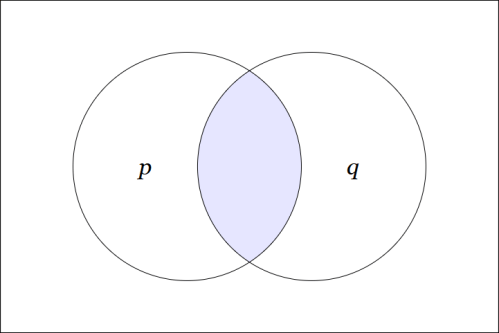
In the field picture a proposition $f : X \to \mathbb{B}$ becomes a scalar field, that is, a field of values in $\mathbb{B}.$

For example, consider the logical conjunction $pq : X \to \mathbb{B}$ shown in the following venn diagram.

$\text{Conjunction}~ pq : X \to \mathbb{B}$

Each of the operators $\mathrm{E}, \mathrm{D} : X^\bullet \to \mathrm{E}X^\bullet$ takes us from considering propositions $f : X \to \mathbb{B},$ here viewed as scalar fields over $X,$ to considering the corresponding differential fields over $X,$ analogous to what in real analysis are usually called vector fields over $X.$

Resources

cc: Academia.edu • Cybernetics • Structural Modeling • Systems Science
cc: Conceptual Graphs • Laws of Form • Ma^thstodon • Research Gate

	Survey of Semiotics,… on Sign Relations • Semiotic Equi…
	Survey of Semiotics,… on Sign Relations • Semiotic Equi…
	Sign Relations • Sem… on Survey of Semiotics, Semiosis,…
	Survey of Semiotics,… on Sign Relations • Semiotic Equi…
	Sign Relations • Sem… on Survey of Semiotics, Semiosis,…
	Sign Relations • Sem… on Survey of Semiotics, Semiosis,…
	Survey of Semiotics,… on Sign Relations • Semiotic Equi…
	Sign Relations • Sem… on Survey of Semiotics, Semiosis,…
	Survey of Semiotics,… on Systems of Interpretation •…
	Survey of Semiotics,… on Sign Relations, Triadic Relati…

M	T	W	T	F	S	S
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30