Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6) • (7) • (8) • (9)

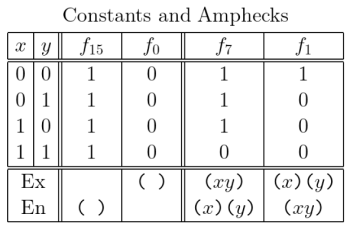
After the four orbits of self‑dual logical graphs we come to six orbits of dual pairs.  In no particular order of importance, we may start by considering the following two.

• The logical graphs for the constant functions and are dual to each other.
• The logical graphs for the ampheck functions and are dual to each other.

The values of the constant and ampheck functions for each and the text expressions for their logical graphs are given in the following Table.

Resources

• Logic Syllabus
• Amphecks • Zeroth Order Logic
• Survey of Animated Logical Graphs
• Survey of Semiotics, Semiosis, Sign Relations

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science