Transformation Rules and Equivalence Classes

The abstract character of the cactus language relative to its logical interpretations makes it possible to give abstract rules of equivalence for transforming cacti among themselves and partitioning the space of cacti into formal equivalence classes.  The transformation rules and equivalence classes are “purely formal” in the sense of being indifferent to the logical interpretation, entitative or existential, one happens to choose.

Two definitions are useful here:

• A reduction is a transformation which preserves equivalence classes and reduces the level of graphical complexity.
• A basic reduction is a reduction which applies to a basic connective, either a node connective or a lobe connective.

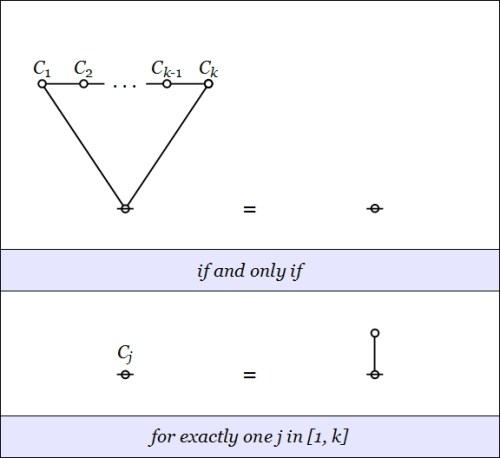
The two kinds of basic reductions are described as follows.

• A node reduction is permitted if and only if every component cactus joined to a node itself reduces to a node.

• A lobe reduction is permitted if and only if exactly one component cactus listed in a lobe reduces to an edge.

That is roughly the gist of the rules.  More formal definitions can wait for the day when we need to explain their use to a computer.

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Theme One Program • User Guide
• Survey of Theme One Program

cc: FB | Theme One Program • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science