Re: Transformations of Logical Graphs • 1

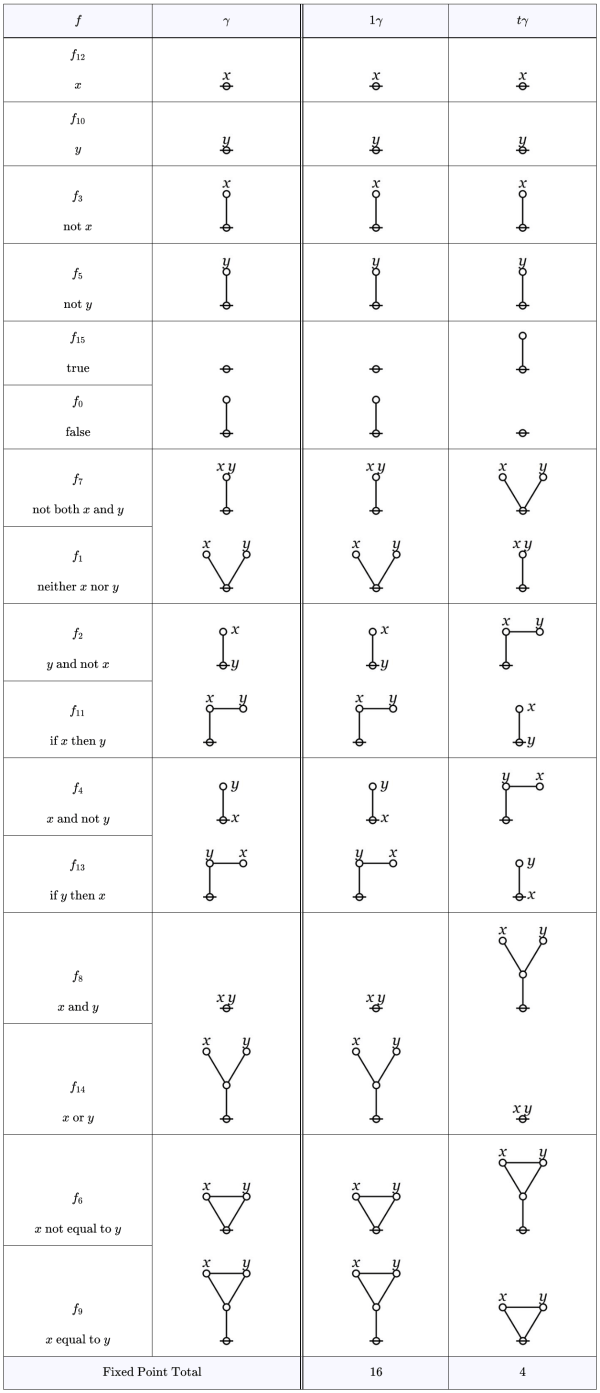
Another way of looking at the dual interpretation of logical graphs from a group-theoretic point of view is provided by the following Table.  In this arrangement we have sorted the rows of the previous Table to bring together similar graphs belonging to the set the similarity being determined by the action of the group   Transformation group theorists refer to the corresponding similarity classes as orbits of the group action under consideration.  The orbits are defined by the group acting transitively on them, meaning elements of the same orbit can always be transformed into one another by some group operation while elements of different orbits cannot.

Scanning the Table we observe the 16 points of fall into 10 orbits total, divided into 4 orbits of 1 point each and 6 orbits of 2 points each.  The points in singleton orbits are called fixed points of the transformation group since they are not moved but mapped into themselves by all group actions.  The bottom row of the Table tabulates the total number of fixed points for the group operations and respectively.  The group identity always fixes all points, so its total is 16.  The group action fixes only the four points in singleton orbits, giving a total of 4.

I leave it as an exercise for the reader to investigate the relationship between the group order the number of orbits and the total number of fixed points

Resources

• Logic Syllabus
• Logical Graphs • First Impressions
• Logical Graphs • Formal Development

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science