Minimal Negation Operators • 2

Posted on August 30, 2017 by Jon Awbrey

Re: Minimal Negation Operators • 1

The brief description of minimal negation operators given in the previous post is enough to convey the rule of their construction.  For future reference, a more formal definition is given below.

Initial Definition

The minimal negation operator \nu is a multigrade operator (\nu_k)_{k \in \mathbb{N}} where each \nu_k is a k-ary boolean function defined by the rule that \nu_k (x_1, \ldots, x_k) = 1 if and only if exactly one of the arguments x_j is 0.

In contexts where the initial letter \nu is understood, minimal negation operators may be indicated by argument lists in parentheses.  In the discussion that follows a distinctive typeface will be used for logical expressions based on minimal negation operators, for example, \texttt{(} x \texttt{,} y \texttt{,} z \texttt{)} = \nu (x, y, z).

The first four members of this family of operators are shown below.  The third and fourth columns give paraphrases in two other notations, where tildes and primes, respectively, indicate logical negation.

Minimal Negation Operators

Resources

cc: Cybernetics • Ontolog Forum • Peirce List • Structural Modeling • Systems Science
cc: FB | Minimal Negation Operators • Laws of Form

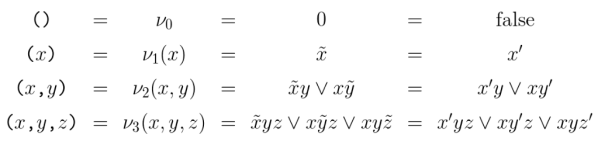
This entry was posted in Amphecks, Animata, Boolean Functions, C.S. Peirce, Cactus Graphs, Differential Logic, Functional Logic, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Semiotics, Venn Diagrams, Visualization and tagged , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.